pierre.sabiy
- 13
- 0
I want to simulate such a system in Simulink.
It is a system of mass between two compression, spring preload. Springs are compressed length of 64 mm to 54 mm. Acts on mass shock 50G for 10ms. The coefficient of spring constant is changed depending on the position and direction of movement mass.
But I can not deal with the equation.
So far I only have such an equation, but probably not correct.
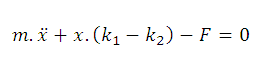
how to calculate such a system?
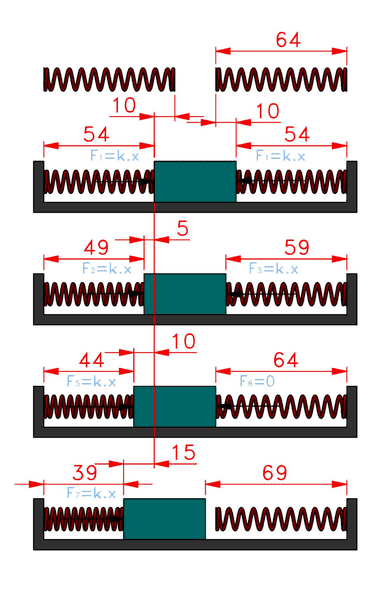
It is a system of mass between two compression, spring preload. Springs are compressed length of 64 mm to 54 mm. Acts on mass shock 50G for 10ms. The coefficient of spring constant is changed depending on the position and direction of movement mass.
But I can not deal with the equation.
So far I only have such an equation, but probably not correct.
how to calculate such a system?