green-fresh
- 14
- 0
hello there!
I was reading about ohm rule in a MIT physics course and they calculate the resistance of a nested spherical shells like this :
and they but the microscopic form of ohm's law which is :
J=\sigma_q E
and
I=A J
so
I=(4 \pi r^2 ) (\sigma_q E)
and
E=-\frac{\partial V}{\partial r}
and he said that the potential must be like this form
V=\frac{C}{r}+D
where : C and D are constant .
so my question is what is this form and why he did that and i could calculate the potential easily :
V_{ab}=\int E . dr.
thank you
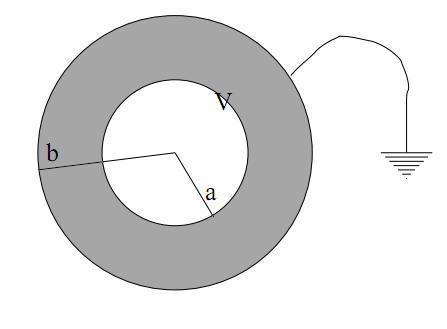
I was reading about ohm rule in a MIT physics course and they calculate the resistance of a nested spherical shells like this :
and they but the microscopic form of ohm's law which is :
J=\sigma_q E
and
I=A J
so
I=(4 \pi r^2 ) (\sigma_q E)
and
E=-\frac{\partial V}{\partial r}
and he said that the potential must be like this form
V=\frac{C}{r}+D
where : C and D are constant .
so my question is what is this form and why he did that and i could calculate the potential easily :
V_{ab}=\int E . dr.
thank you