Hello Rankel,
Let's plot the given points and connect them with line segments:
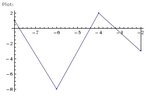
View attachment 1728
As you can see, we have four triangles, two above the $x$-axis, and two below. Beginning on the left, we see the first triangle above the $x$-axis has a height $h$ of 1. Its base $b$ can be found by similarity:
$$\frac{b}{1}=\frac{2}{9}$$
Hence, its area is:
$$A_1=\frac{1}{2}bh=\frac{1}{2}\cdot\frac{2}{9}\cdot1=\frac{1}{9}$$
Moving to the right to the first triangle under the $x$-axis, we see its height is 8. From the first triangle, we know the $x$-coordinate of the left end of its base is:
$$x_1=-8+\frac{2}{9}=-\frac{70}{9}$$
Using similarity, we find the $x$-coordinate of the right end of the base is:
$$x_2=-4-\frac{2}{5}=-\frac{22}{5}$$
Hence the base is:
$$b=-\frac{22}{5}+\frac{70}{9}=\frac{152}{45}$$
And so the area of the second triangle is given by:
$$A_2=\frac{1}{2}bh=\frac{1}{2}\cdot\frac{152}{45} \cdot8=\frac{608}{45}$$
Next, moving to the right to the second triangle above the $x$-axis, we see its height is 2. We know the left end of its base is:
$$x_1=-\frac{22}{5}$$
And, using similarity, we find the right end of the base is at:
$$x_2=-4+\frac{4}{5}=-\frac{16}{5}$$
Hence the length of the base is:
$$b=-\frac{16}{5}+\frac{22}{5}=\frac{6}{5}$$
And so the area of the third triangle is:
$$A_3=\frac{1}{2}bh=\frac{1}{2}\cdot\frac{6}{5}\cdot2=\frac{6}{5}$$
And moving to the second triangle below the $x$-axis, we see its height is 3 and its base is:
$$b=-2+\frac{16}{5}=\frac{6}{5}$$
Thus, its area is:
$$A_4=\frac{1}{2}bh=\frac{1}{2}\cdot\frac{6}{5}\cdot3=\frac{9}{5}$$
So, we may now state:
$$\int_{-8}^{-2} f(x)\,dx=A_1-A_2+A_3-A_4=\frac{1}{9}-\frac{608}{45}+\frac{6}{5}-\frac{9}{5}=-14$$
As a check, we may find the linear equations describing the lines segments and then integrate over the appropriate intervals. The line passing through the points $\left(x_1,y_1 \right)$ and $\left(x_2,y_2 \right)$ is given by:
$$y=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1 \right)+y_1$$
Thus, we find the following:
$$\overline{AB}\implies y=\frac{-8-1}{-6+8}(x+8)+1=-\frac{9}{2}x-35$$
$$\overline{BC}\implies y=\frac{2+8}{-4+6}(x+6)-8=5x+22$$
$$\overline{CD}\implies y=\frac{-3-2}{-2+4}(x+4)+2=-\frac{5}{2}x-8$$
And so we have:
$$\int_{-8}^{-2} f(x)\,dx=\int_{-8}^{-6} -\frac{9}{2}x-35\,dx+\int_{-6}^{-4} 5x+22\,dx+\int_{-4}^{-2} -\frac{5}{2}x-8\,dx$$
$$\int_{-8}^{-6} -\frac{9}{2}x-35\,dx=-\left[\frac{9}{4}x^2+35x \right]_{-8}^{-6}=$$
$$-\left(\left(\frac{9}{4}(-6)^2+35(-6) \right)-\left(\frac{9}{4}(-8)^2+35(-8) \right) \right)=-\left(-129+136 \right)=-7$$
$$\int_{-6}^{-4} 5x+22\,dx=\left[\frac{5}{2}x^2+22x \right]{-6}^{-4}=$$
$$\left(\frac{5}{2}(-4)^2+22(-4) \right)-\left(\frac{5}{2}(-6)^2+22(-6) \right)=-48+42=-6$$
$$\int_{-4}^{-2} -\frac{5}{2}x-8\,dx=-\left[\frac{5}{4}x^2+8x \right]{-4}^{-2}=$$
$$-\left(\left(\frac{5}{4}(-2)^2+8(-2) \right)-\left(\frac{5}{4}(-4)^2+8(-4) \right) \right)=-\left(-11+12 \right)=-1$$
And so we find:
$$\int_{-8}^{-2} f(x)\,dx=-7-6-1=-14$$
And this checks with our previous result.