ardentmed
- 158
- 0
Hey guys,
I have a couple of questions about the problem set I'm doing at the moment. Although I was able to solve most of these, I'm doubting quite a few of my responses.
http://i.share.pho.to/f7d7efe6_o.pnghttp://i.share.pho.to/82c05629_o.png
http://i.share.pho.to/d6f76bb6_o.png
http://i.share.pho.to/4a3c738c_o.png
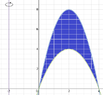
For the first one, I split up the integral into two parts and obtained three different functions from the three coordinates, then added the area obtained from the two integrals, 4 and 6 respectively, to get 10.
For the second one, I used the formula for a semi-circles area, $\pi * r ^2 / 2 and obtained 9/8 * $\pi for the area, then integrated it from y=2 to y=0 with respect to y and obtained 9/4 * $\pi in total. This is because the triangle has a base of 3 metres in length, so I presumed that I could use that (and divide it by 2) to get the radius of the semi-circle. Albeit, I'm really not too sure about this one
For the third one, I just used the cylindrical shells method with (2+x) as the radius, expanded the integral, and integrated. I got ~268.083 as the answer.
For the fourth one, I got 29 $\pi / 30 for both answers, so I'm pretty sure I got it right.
For number eight, I integrated 245,000 $\pi * x from 0.3m to 1.5 metres since that is how far the water must travel to get out of the tub. I ended up getting 264,000 Joules, albeit I feel as if I may have made an error somewhere along the way.
Number nine should have been relatively easy, and is a simple average value question, so it's just 1/(b-a) * \int_{}^{} \,d , which gave me 24 degrees celsius.
Thanks in advance for the help, guys. I really appreciate it
I have a couple of questions about the problem set I'm doing at the moment. Although I was able to solve most of these, I'm doubting quite a few of my responses.
http://i.share.pho.to/f7d7efe6_o.pnghttp://i.share.pho.to/82c05629_o.png
http://i.share.pho.to/d6f76bb6_o.png
http://i.share.pho.to/4a3c738c_o.png
For the first one, I split up the integral into two parts and obtained three different functions from the three coordinates, then added the area obtained from the two integrals, 4 and 6 respectively, to get 10.
For the second one, I used the formula for a semi-circles area, $\pi * r ^2 / 2 and obtained 9/8 * $\pi for the area, then integrated it from y=2 to y=0 with respect to y and obtained 9/4 * $\pi in total. This is because the triangle has a base of 3 metres in length, so I presumed that I could use that (and divide it by 2) to get the radius of the semi-circle. Albeit, I'm really not too sure about this one
For the third one, I just used the cylindrical shells method with (2+x) as the radius, expanded the integral, and integrated. I got ~268.083 as the answer.
For the fourth one, I got 29 $\pi / 30 for both answers, so I'm pretty sure I got it right.
For number eight, I integrated 245,000 $\pi * x from 0.3m to 1.5 metres since that is how far the water must travel to get out of the tub. I ended up getting 264,000 Joules, albeit I feel as if I may have made an error somewhere along the way.
Number nine should have been relatively easy, and is a simple average value question, so it's just 1/(b-a) * \int_{}^{} \,d , which gave me 24 degrees celsius.
Thanks in advance for the help, guys. I really appreciate it
Last edited: