Volumes Definition and 192 Threads

Volume is the quantity of three-dimensional space enclosed by a closed surface, for example, the space that a substance (solid, liquid, gas, or plasma) or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces.
Three dimensional mathematical shapes are also assigned volumes. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures (such as lines) and two-dimensional shapes (such as squares) are assigned zero volume in the three-dimensional space.
The volume of a solid (whether regularly or irregularly shaped) can be determined by fluid displacement. Displacement of liquid can also be used to determine the volume of a gas. The combined volume of two substances is usually greater than the volume of just one of the substances. However, sometimes one substance dissolves in the other and in such cases the combined volume is not additive.In differential geometry, volume is expressed by means of the volume form, and is an important global Riemannian invariant.
In thermodynamics, volume is a fundamental parameter, and is a conjugate variable to pressure.

View More On Wikipedia.org
Recent contents Top users
  1. C

    Trouble solving for end state of two control volumes in a rigid tank

    TL;DR Summary: Struggling to structure the problem and derive an analytical solution for gas expanding into other gas in a rigid tank. Preferred formulation is fixed control volumes. This is not a homework problem. The problem: Two control volumes (A and B) are in a rigid tank filled with air...
  2. mncyapntsi

    Confused about polar integrals and setting up bounds

    So I want to subtract the two surfaces, right? I really don't know where to start... I am guessing this would be some sort of triple integral, however I am very confused with the bounds. Any help would be greatly appreciated! Thanks!!
  3. N

    Pressure drop through volumes of compressible fluid

    Thanks for your response. I'm trying to estimate the pressure in the cavity, i.e. P2. I know the areas, A1 which in practicality is an annulus and A2 which is a 600m pipe with i/d 8mm. I would like to initially understand how to calculate the pressure drop across the annulus. At the moment I'm...
  4. N

    MHB Calculating Sand Volume for a Cylindrical Containment Vessel

    A spherical pressure vessel with a diamter of 10 m is tightly enclosed in a cylindrical containment vessel with the sphere just touching on all 4 sides . Additional protective material (assume is sand ) is added to the cyclinder to provide additional support .How much sand is required so that...
  5. C

    Most compressible volumes: synthetic fibre versus natural eider down?

    I'm just purchasing some exped kit including coats and sleeping bags containing down as the insulator. The key superlative of down is that it can be compressed and then recovers to a big volume. If one ounce of material re-expands, after compression, to 800 cubic inches then this is called '800...
  6. E

    B Control volumes and Reynolds transport theorem

    If we consider a system of fixed mass as well as a control volume which is free to move and deform, then Reynolds transport theorem says that for any extensive property ##B_{S}## of that system (e.g. momentum, angular momentum, energy, etc.) then$$\frac{dB_{S}}{dt} = \frac{d}{dt} \int_{CV} \beta...
  7. O

    I Converting Unit Cell Volumes of Minerals to Density

    I'm modelling the interiors of core-dominated (exo)planets. The EoS I use in my calculations are mostly either a Birch-Murnaghan formulation or a Mie-Grüneisen-Debye formulation. In either case, the ambient density ρ0 at ambient pressure and temperature are required for the implementation...
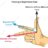
  8. WateryFungi

    Engineering Thermodynamics - Control Volumes find final temperature

    Hi I'd like to know if my current approach to the problem has any issues. My attempt: Balancing the equation: Qin + Win +mΘout = Qout + Wout + mΘout Qin+m(hin + v2in/2 + gzin) = m(hout + v2out/2 + gzout) Wflow + ΔU + m(hin) = m(hout) I factored out the mass: wflow + Δu + hin = hout And I used...
  9. J

    Quantum Does a draft of Zeidler's missing volumes of his QFT series exist?

    I enjoyed a lot the three first volumes of Zeidler's planned series of 6 books on QFT. Unfortunately, he passed away too soon. However, it is clear from reading the first three books, that an outline of the next books in the series was already planned. Is there a draft, containing the basis of...
  10. R

    Volumes in different dimensions

    I would assume that it has some area even if it is really really small. But I guess a line implies that the left and right boundaries are going to the middle an infinite amount, so it has area =0? does anyone get what I mean?
  11. S

    Other Smirnov's "Course of Higher Mathematics"

    Hi, I recently have rekindled my love for mathematics while in University for Political Science. I have reviewed all of my old pre cal books, but now I want to start learning Calculus eventually on to more difficult things like PDEs and things of that nature. I like having a series of textbooks...
  12. zul8tr

    Hydrostatic force on identical containers filled with equal volumes of water

    In the sketch are 2 identical containers filled with equal volumes of water. Which has a greater absolute vertical force only on the conical wall and by what relative amount? Not a classroom or homework problem.
  13. K

    Finding the ratio of the volumes of a cube and a sphere

    Homework Statement Homework Equations Volue of a sphere: ##~\displaystyle V=\frac{4}{3}\pi r^3## Area of a sphere: ##~\displaystyle A=4\pi r^2## Minimum/Maximum occurs when the first derivative=0 The Attempt at a Solution The fixed area is k, the edge is a: $$6a+4\pi...
  14. S

    Calculating 3D Cylinder Volumes & Areas With Constants

    Homework Statement Let r be a positive constant. Consider the cylinder x2 + y2 ≤ r2, and let C be the part of the cylinder that satisfies 0 ≤ z ≤ y. (1) Consider the cross section of C by the plane x = t (−r ≤ t ≤ r), and express its area in terms of r, t. (2) Calculate the volume of C...
  15. T

    I Can Infinitesimal Volumes Be Arbitrary Shapes?

    In physics we often use objects with infinitesimal volume. An example is the infinitesimal volumes that we use to calculate the electrostatic field knowing the charge distribution. Very often in the books i studied these infinitesimal elements are represented as infinitesimal cubes. My question...
  16. T

    Quantum Weinberg's 3 Volumes too difficult?

    I'd like to hear opinions from those who have already some experience on Quantum Field theory, what do they think of Weinberg's 3 volumes, whether they are so hard compared to other books or not. It happens that I have been reading some books on QFT, the last being Ryder's book from 1996. I...
  17. S

    B Volumes and Hyper Volumes Related Special Relativity

    How can volumes and hypervolumes be related to Einstein's theory of special relativity and to quantum mechanics? Also, can volumes and hypervolumes of objects be used for modeling how different scenarios can change over time? Oh yeah, and hi my name is Sasha Jaffarove!
  18. H

    Volumes of a Buffer using Henderson-Hasselbalch?

    Homework Statement Calculate the volume of 0.10M phosphate solution to mix to prepare 100mL of a buffer with pH 6.0 starting with 0.10M stock solutions of NaH2PO4 and Na2HPO4. The pKa for this reaction is 7.21. Homework Equations pH=pHa+log( [A-]/[HA]) The Attempt at a Solution When I did it...
  19. M

    MHB Gay-Lussac's Law of combining volumes

    50 cm^3 of nitrogen combine with 150 cm^3 of hydrogen gas to form 100 cm^3 of ammonia. Does this agree with gay lussacs law of combing volumes?. Explain your answer. i feel the answer is yes but I can not give the reason why?
  20. M

    I Volumes of n-Spheres: Intuition & Calculations

    I'm trying to wrap my head around how higher dimensions work. Not over some academic pursuit, merely curiosity(which started with me discovering this neat recurrence relation). Given that the surface area of a sphere is an object of 1 dimension lower. So on a 3-sphere, the surface area is a...
  21. M

    Calculation of specific volumes

    Homework Statement 300 kPa pressure and v=0.5 m3/kg. The state is fixed. I should find the temperature and quality if defined. Table values for temperature T P vf vfg vg 130C 270.1kPa 0.001070...
  22. M

    Specific volumes of a saturated substance due to pressure

    I cannot understand why specific volume of a saturated liquid rises when pressure rises, specific volume of saturated vapor reduces when pressure rises. This made me remember buckingham-pi theorem. Is there any equational approach or formulation that show this? Thank you.
  23. deepak tayade

    Meshing Volumes 1 & 2: Need Assistance!

    i want to Mesh volume1 of 0.250 X 0.180 X 0.005 (solid 45) and another volume2 of 0.050 X 0.020 X 0.005 (solid 5)placed at the centre & on top of volume 1... i m not able to mesh please assist...
  24. S

    Control Volumes - Fluid Mechanics

    After doing extensive research, I am still confused about Control Volumes. Say that there is water flowing into a cup at a steady rate, and I am required to illustrate the momentum and mass flows, as well as the forces, how would I approach this? I have seen examples of Control Volumes but they...
  25. R

    I Why equal volumes of diferent gases have the same number of molecules @ STP?

    Hi, A silly techiniacal, very basic but logical question. Trying to understand since long but unable to justify myself. Can u help? Deferent gases have deferent molecular size, then how is it possible that equal volume of deferent gases have same numbers of volume at standard temperature &...
  26. Kirito123

    Finding the Volume of Cones and Cylinders Using Known Values

    Homework Statement Homework Equations volume of cone = pi(r)2h / 3 volume of cylinder = pi(r)2h The Attempt at a Solution How can I do this, all they give is the volume and we know the value of pi ( 3.14159). I tried but you can't do it without knowing at least the radius or the height.
  27. Kirito123

    Need help understanding volumes of cones

    Homework Statement This was a example but I didn't quite understand it, I don't know how they ended up with 565.49 every time I try I get some random other number. Homework Equations The Attempt at a Solution So this is how i do it. Pi (6) 2 (15)/3 So first I multiply 3.14 (pi) by 6. so...
  28. V

    Volumes in Charge symmetry anf distribution problems

    Hi everyone, I am self-studying Electricity and Magnetism. I have a good grasp in Calculus, but still I am confused on how to figure out volumes of arbitrary figures(rest is easy). I know it's a bit silly. I mean how do we know how to choose a figure (like in case of hemisphere, you imagine...
  29. N

    Simpson's rule with changing volumes

    Hi there, Homework Statement I am doing a simulation of a free-fall lifeboat trajectory into the ocean and there is a part where i need to get the volume of the lifeboat to obtain its buoyancy force. Buoyancy force is proportional to the immersed volume of the body and this volume can be...
  30. G

    I Confusion on the Volumes of Solids of Revolution

    I've been trying to figure out why you can't use the average value of a function to determine the volume of a solid of revolution. As an example: Trying to find the volume of a solid of revolution on y=√x from 0 to 1 around the x-axis. The definite integral is 2/3, which divided by one is...
  31. M

    Finding Volumes of Sphere & Circular Cone: Alpha from 0 to Pi

    Use an appropriate volume integral to find an expression for the volume enclosed between a sphere of radius 1 centered on the origin and a circular cone of half-angle alpha with its vertex at the origin. Show that in the limits where alpha = 0 and alpha = pi that your expression gives the...
  32. M

    Calc II - Disk vs Shell method different volumes

    So I'm getting ready for an exam on tuesday, and I'm using each method for volumes of revolutions for every problem but I'm not getting the same answers. So, let's use this as an example: y = 5x; the shaded region is from [1,2] Using the disk method (about the x-axis) I find: R(x) = 5x; r(x)...
  33. 1729

    Determining the ratio of volumes

    Homework Statement A crown is made out of silver and gold. Its weight is 58.8 N in air, and 54.8 N when submerged in water. What is the ratio of ##V_{\mathrm{gold}}## to ##V_{\mathrm{silver}}## in the crown? ##\rho_{\mathrm{gold}}=19300\frac{\mathrm{kg}}{\mathrm{m^3}}##...
  34. P

    How Do You Find Volumes of Solids of Revolution in These Complex Scenarios?

    I have a few questions about finding volumes of solids of revolution (in a typical first year single variable calculus course). 1) I can rotate any region about any horizontal/vertical axis. How exactly do I rotate a region about a line that is neither horizontal nor vertical (##y = x - 1## for...
  35. Q

    Volumes at C and D in a Carnot cycle

    Homework Statement A Carnot cycle, shown in Fig. 20-7, has the following conditions: Va = 7.5 L, Vb = 15 L, TH = 470°C, and TL = 260°C. The gas used in the cycle is 0.50 mil of a diatomic gas, y = 1.4. Calculate (a) the pressures at a and b; (b) the volumes at c and d. (The rest of the...
  36. U

    MHB Calculating Average Fees and Transaction Volumes Word Problem

    If I have 415 transactions and know there are only two types of transactions (H&L) with a total average fee of 1.4 and I know transaction H has an average fee of 1.20 can I calculate the average fee for L and the individual transaction volumes for both H and L? I should also note that the total...
  37. cvex

    How to get the laplacian of a scalar field?

    Hi, I am trying to calculate the laplacian of a scalar field but I might actually need something else. So basically I am applying reaction diffusion on a 2d image. I am reading the neighbours, multiplying them with these weights and then add them. This works great. I don't know if what I am...
  38. gracy

    Exploring Avogadro's Law: Equal Molecules, Equal Volumes?

    Avogadro's Law states that 'equal volumes of gases at the same temperature and pressure contain the same number of molecules' or moles of gas. My question is ,will it be correct if we reverse the law, I mean if gases of equal moles at the same temperature and pressure will have equal volumes,is...
  39. Meadow_Lark

    Henderson Hasselbalch Buffers and Volumes

    Homework Statement You have 725 mL of an 0.55 acetic acid solution. What volume (V) of 1.30 M NaOH solution must you add in order to prepare an acetate buffer of pH = 4.99? ( The pKa of acetic acid is 4.76.) [/B] Homework Equations pH = pKa + log A/HA Ratio of A- to HA = 10^(pH-pKA)[/B]The...
  40. oreo

    Questions on Buoyancy: Equal Volumes, Different Depths

    I have a little confusion regarding bouyancy. Suppose two objects fully immersed in liquid having equal volumes, one close to surface but other at greater depth. As both displace equal volumes of water therefore they should be facing equal bouyant forces. But as the object which is at greater...
  41. RJLiberator

    Volumes of Revolution Question

    Homework Statement Let R be the region bounded by the curves y=0 and y=x^2+x between x=0 and x=1. Compute the volume of the solid of revolution obtained when R is rotated about the axis y=-1. Homework Equations Disc method: integral of pi*r^2 = volume from the bounds The Attempt at a Solution...
  42. RJLiberator

    Volumes of Revolution with e^-x

    Homework Statement Compute the region R in the first quadrant between y=e^(-x), x=0, and y=0. Compute using shells, the volume V of solid around the y-axis. Homework Equations Volume =integral of bounds 2pi*radius*height The Attempt at a Solution First I drew the graph. This graph really is...
  43. L

    Volumes of Irregular Shapes by Integration

    Hi all, Is it possible to determine the volume of a shape where, in the x and y dimensions, the shape is described by an equation, and then its elevation is described by another equation? An example would be a parabola in the x-y plane whose elevation is based on another parabolic...
  44. I

    MHB Volumes of Solids of Revolution using Shells

    my final is tomorrow and my instructor gave a list of questions that will be similar to the ones on the final exam and i want to see how they should be done properly. I've been working on other problems but i can't get past these ones. thanks determine the volume using the shell method $y=5|x|$...
  45. A

    MHB Calculus II Volumes of Revolution and Basic Integration Questions

    Hey guys, I have a couple of questions about the problem set I'm doing at the moment. Although I was able to solve most of these, I'm doubting quite a few of my responses. http://i.share.pho.to/f7d7efe6_o.pnghttp://i.share.pho.to/82c05629_o.png http://i.share.pho.to/d6f76bb6_o.png...
  46. W

    Models for Determining Volumes and Surface Areas

    When we generate solid by rotating a curve around an axis, we use "slabs" of cylinders to approximate the volume of this solid of revolution. When we want the find the surface area, we instead use "slabs" of conical frustums (ie. the slope of the differential length of curve is taken into...
  47. J

    Find Volumes of Rotated Solids in AP Calc

    Homework Statement 1. R is the shaded region in the 1st quadrant bounded by the graph of y=4ln(3-x), the horizontal line y=6, and the vertical line x=2 Find the volume of the solid when revolved about the horizontal line y=8 2. Let R be the region in the 1st quadrant enclosed by the graphs of...
  48. C

    Volumes of solids of revolution with infinity

    Homework Statement Consider the infinite region in the first quadrant between the curve y=e^-5x and the x-axis. Find area= 1/5 (got this part) Compute the volume of the solid generated by revolving the region about the x-axis: Compute the volume of the solid generated by revolving the...
  49. J

    Calculus Definite Integrals: Volumes by Washer Method

    Homework Statement Using Washer Method: Revolve region R bounded by y=x^2 and y=x^.5 about y=-3 Homework Equations V= integral of A(x) from a to b with respect to a variable "x" A(x)=pi*radius^2 The Attempt at a Solution pi(integral of (x^.5-3)^2 -(x^2)^2-3) from 0 to 1 with...
  50. P

    Calculating Volume with Volumes of Revolution: Triangle Rotated about x = -2

    Homework Statement Calculate the volume obtained by rotating the triangle bounded by y = 0, y = x, and y = 2 - x, about the line x = -2. You may use either horizontal or vertical rectangles. The Attempt at a Solution So since this is a triangle, I tried to split up the volume down to...
Back
Top