Can all bending moments be represented by force couples?

[etotheipi]

A bending moment about an axis passing through a cross section arises due to an uneven distribution of stress across the cross section, like so:

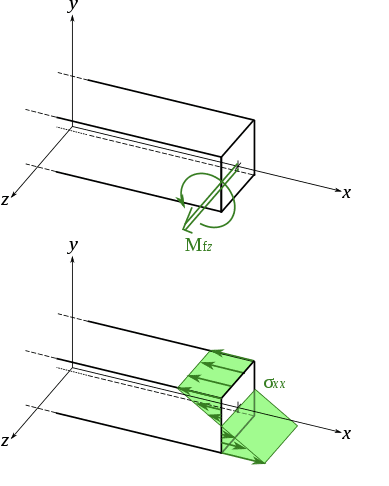
I have read that any given bending moment is equivalent to a force couple applied about that axis. That is to say that the curly moment arrow on a FBD represents a force couple producing a moment. The upshot is that the moment of a couple is the same about any parallel axis, which can be useful for problem solving.

However, one engineering reference page said this

Thus, the internal forces in any cross section of a symmetric member in pure bending are equivalent to a couple.

I don't see why the internal forces on a non-symmetric member would not be equivalent to a couple? I wondered if you would agree? Thanks!

 

[Dr.D]

A moment is a couple. The fact that the particular bending moment is internal to a member does not change that fact. Thus the answer is, yes, any bending moment is equal to a couple.

 

[Lnewqban]

Please, see:
https://en.m.wikipedia.org/wiki/Couple_(mechanics)

 

[etotheipi]

This thread is very old! However...

A moment is a couple.

depends on how you have defined 'moment'. A moment $\mathbf{M} = \boldsymbol{x} \times \mathbf{F}$ is not a couple (and it is origin dependent), whilst a moment $\mathbf{M} = \boldsymbol{x}_1 \times \mathbf{F} + \boldsymbol{x}_2 \times (-\mathbf{F})$ is a couple.

The question I think I was really asking is: the bending moment in a beam is given by$$M_y = \frac{E}{R} \int x^2 df$$and we wonder whether it is a true 'couple', i.e. whether it's origin independent. And I think the answer to that is in this case, for a bending moment a beam, yes.