Can Derivative Methods Determine the Correct Angle in Physics Problems?

[Tapias5000]

Homework Statement

Determine the moment of the force with respect to point O as a function of θ . for what value of θ in the range between 0° and 180° is the moment at its maximum? what is the value of the moment in this case?

Relevant Equations

Mo= R x F

This is the image of the problem:

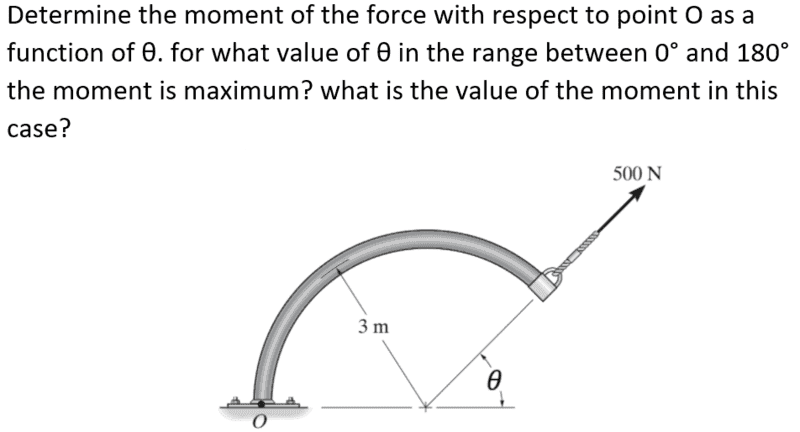
I tried to solve it and I got the following is it correct?

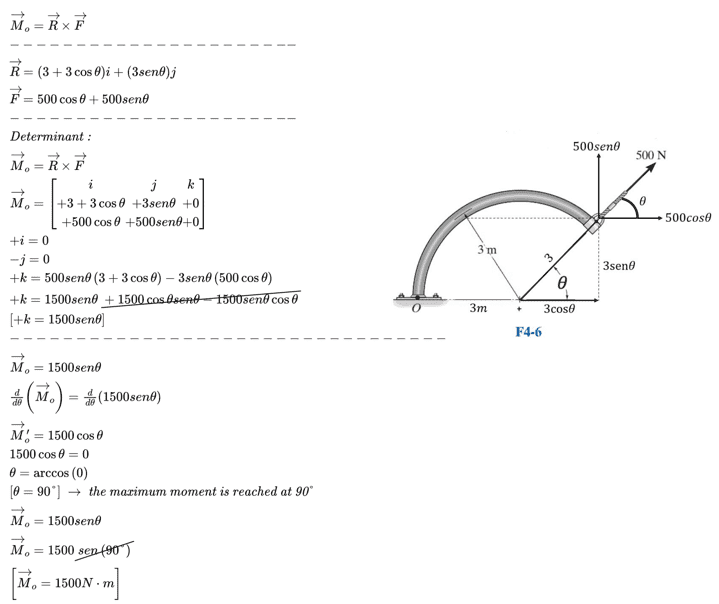
derive and equal to 0 because it is between an angle of 0 and 180° is this statement correct?

 

[haruspex]

Looks fine, though you should specify units everywhere, e.g. $1500\sin(\theta)Nm$.

You can take the point of action of a force as anywhere along its line of action, so it is simpler to consider the force acting at the centre of the arc. The horizontal component then has no moment about O, and you can write the answer down immediately.

Btw, you put "momentum" in the title instead of "moment".

 

[Tapias5000]

Looks fine, though you should specify units everywhere, e.g. $1500\sin(\theta)Nm$.

You can take the point of action of a force as anywhere along its line of action, so it is simpler to consider the force acting at the centre of the arc. The horizontal component then has no moment about O, and you can write the answer down immediately.

Btw, you put "momentum" in the title instead of "moment".

ok, but I still need to find the angle, is the statement I said correct to find it?

 

[haruspex]

ok, but I still need to find the angle, is the statement I said correct to find it?

Yes.