How to determine the car's deceleration at a point along a curve?

[simphys]

Homework Statement

When the car reaches point A it has a speed of $25m/s$. If the brakes are applied, its speed is reduced by $a_t = -\frac 14 \sqrt{t} \frac {m}{s^2}$. Determine the magnitude of acceleration of the car just before it reaches point $C$.

Relevant Equations

$s = R*\theta$

So I get the exercise and all and have just solved it. But .. I kind of very very intuitively determined $\theta$ to also be the angle for the circular sector.
The problem here is that my geometry bag is very weak, I didn't have any geometry in HS, will fix that sooner or later but anyway. so... My question is.. how do I 'actually' derive that the angle of the circular sector equals $\theta = 30$ degrees in such situations?

Thanks in advance.
My thought process was, okay so theta keeps increasing as we move along the circular segment which probably implies that the angle of the sector $= \theta$

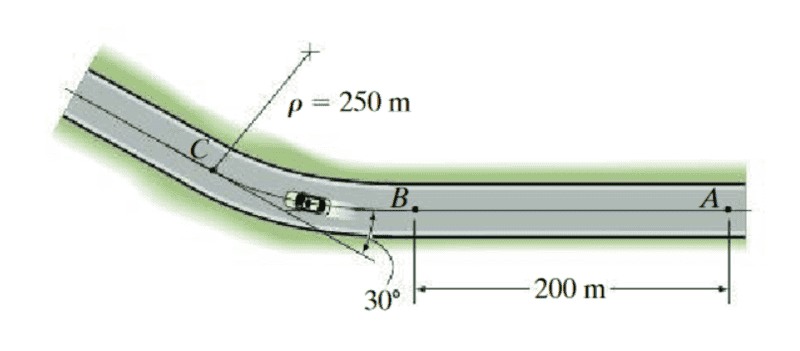
note: the circular path is from B --> C. It might not look as it is due to the placement of the center of curvature, but it is.

 

[BvU]

So I get the exercise and all

Good. We can't: the image is severly blurred and illegible.
What is the complete problem statement ?

 

[simphys]

Good. We can't: the image is severly blurred and illegible.
What is the complete problem statement ?

I have written in the problem statement section?? what do you mean
The picture is just for the drawing of the situation.

 

[simphys]

Good. We can't: the image is severly blurred and illegible.
What is the complete problem statement ?

it's reaaaal bad.. let me take another one.

 

[simphys]

Good. We can't: the image is severly blurred and illegible.
What is the complete problem statement ?

edited, thank you.

 

[BvU]

that the angle of the sector =θ

That's correct. The heading of the car changes bij 30 degrees.

[edit] The $\rho=250\ \text m$ appears to be not to scale (the distance to $B$ is much more than to $C$ ). A bit misleading.

$\$

 

[simphys]

That's correct. The heading of the car changes bij 30 degrees.

$\$

yes but I don't get why that implies that the angle of THE CIRCULAR SEGMENT also equals $30$ degrees.

 

[simphys]

That's correct. The heading of the car changes bij 30 degrees.

[edit] The $\rho=250 \text m$ appears to be not to scale (the distance to $B$ is much more than to $C$ ). A bit misleading.

$\$

yep I noted it under the picture already :), thank you for mentioning.

 

[sophiecentaur]

yes but I don't get why that implies that the angle of THE CIRCULAR SEGMENT also equals $30$ degrees.

The tangent to the circle is always at right angles to the radius. Increase one and the other will increase by the same amount/. Is that your problem?

 

[simphys]

The tangent to the circle is always at right angles to the radius. Increase one and the other will increase by the same amount/. Is that your problem?

Oh, so basically.. the angle b/n two tangents is equivalent to the angle between normals of the tangents? Is that what you meant? And then from this we know that it's going to be the angle of the circular segment.

 

[sophiecentaur]

Oh, so basically.. the angle b/n two tangents is equivalent to the angle between normals of the tangents? Is that what you meant? And then from this we know that it's going to be the angle of the circular segment.

Yes. It's simple geometry. The two lines are fixed with 90° between them. Increase one by x and the other will increase by x. Imagine a set square rotating around a pivot on one arm. Every part of it will be rotating by the same angle

 

[simphys]

Yes. It's simple geometry. The two lines are fixed with 90° between them. Increase one by x and the other will increase by x. Imagine a set square rotating around a pivot on one arm. Every part of it will be rotating by the same angle

unfortunately not so simple for me
but yeah I kind of get it now I think, thanks a lot.

 

[nasu]

There is a theorem in geometry: angles with perpendicular sides are equal. This means that if the sides of one angle are each perpendicular to one of the sides of the other angle, the two angles are equal. It is quite useful in physics problems.

 

[simphys]

There is a theorem in geometry: angles with perpendicular sides are equal. This means that if the sides of one angle are each perpendicular to one of the sides of the other angle, the two angles are equal. It is quite useful in physics problems.

Thank you, I just realize that I do the exact same thing with the mg-force, I always translate the perpendicular axis on the other axis that has slope i.e. if the x-axis is rotated to have a slope-angle --> the y-axis will also rotate in the same amount in the same direction. From this I then know that at which side the angle'll be for the mg-force.

 

[sophiecentaur]

There is a theorem in geometry: angles with perpendicular sides are equal. This means that if the sides of one angle are each perpendicular to one of the sides of the other angle, the two angles are equal. It is quite useful in physics problems.

Oh dear. Whatever is an angle with a perpendicular side? I'm sure you are referring to something that I learned over sixty years ago but I can't think what it is.

 

[simphys]

There is a theorem in geometry: angles with perpendicular sides are equal. This means that if the sides of one angle are each perpendicular to one of the sides of the other angle, the two angles are equal. It is quite useful in physics problems.

@nasu wait.. you are asuming another, is this one by chance? because these are really the only two that I know to be quite honest just as they're needed a lot indeed. let me show ya.

 

[simphys]

so from that theorem we get $\phi$ == $\theta$, correct?

 

[nasu]

Look at the left hand side of the image linked below. This is what I was talking about.
https://etc.usf.edu/clipart/48200/48228/48228_angperpsides.htm
The angles 7 and and 1 in the fiure on the left hand side are like this and they are equal. Each side of the angle 7 is perpendicular to one od the two sides of the angle 1. The sides are perpendicluar and not the angles.

 

[simphys]

Look at the left hand side of the image linked below. This is what I was talking about.
https://etc.usf.edu/clipart/48200/48228/48228_angperpsides.htm

thank you that is indeed what I use (but intuitively) to determine the angle for the mg-force on a slope.

 

[nasu]

Oh dear. Whatever is an angle with a perpendicular side? I'm sure you are referring to something that I learned over sixty years ago but I can't think what it is.

It is long ago, true. I learned about it in grade 7 or 8. But I used it many times in physics problems so it stayed fresh. And I tell about it to the first years students who nowadays have almost no geometry in high school.

 

[simphys]

Oh dear. Whatever is an angle with a perpendicular side? I'm sure you are referring to something that I learned over sixty years ago but I can't think what it is.

hahahaha

 

[simphys]

It is long ago, true. I learned about it in grade 7 or 8. But I used it many times in physics problems so it stayed fresh. And I tell about it to the first years students who nowadays have almost no geometry in high school.

well @nasu to be honest, my problem was that I didn't have math for approx. 1.5 years for the last 3 years(including geometry) and next to that I didn't have any science and also my Math was only 2 hrs a week.
So it's basically all self-teaching, but haven't reached geometry yet. Skipped it due to time constraints the past year.

 

[sophiecentaur]

View attachment 304351
so from that theorem we get $\phi$ == $\theta$, correct?

That can only be correct if the top and bottom lines are parallel. For any other angle they are not equal. I think you are trying to apply properties of similar triangles but is something missing in the diagram (on the top left edge of the green bit)?

And I tell about it to the first years students who nowadays have almost no geometry in high school.

You seem to be telling them something that's wrong. Euclidean Geometry is totally self consistent and everything fits the rules. What actual rule are you trying to apply here?

 

[sophiecentaur]

hahahaha

You are laughing but what I learned was the real deal. You seem to be making some of your stuff up and that is disastrous in pure geometry. If you can't prove it from first principles it's wrong. Can you prove what you are claiming about what's on the green paper?

 

[simphys]

You are laughing but what I learned was the real deal. You seem to be making some of your stuff up and that is disastrous in pure geometry. If you can't prove it from first principles it's wrong. Can you prove what you are claiming about what's on the green paper?

I am sorry.. but have you read what I have said.. I have NEVER studied geometry (yet). so I do NOT know those first principle derivations. I know that it is important in physics, but I'll come that later on as I have referred to in post ##22

So inevitably as I haven't studied the real deal yet, I will make assumption that are just wrong ain't that right?

 

[nasu]

You seem to be telling them something that's wrong. Euclidean Geometry is totally self consistent and everything fits the rules. What actual rule are you trying to apply here?

Why is it wrong? It is part of Euclidian geometry.
https://etc.usf.edu/clipart/70000/70087/70087_anglesum.htm
You mean that they can also be supplementary? This does not make it wrong. We are not talking proof of a geometrical theorem but just the use of a tool to figure angles in physics problems.

 

[sophiecentaur]

Why is it wrong?

It's wrong because your green diagram is not the same as the diagram in the link. Only one of your pairs of sides are perpendicular whereas both pairs of sides are perpendicular in the link diagram. A'C' and AC are perpendicular but also AB and A'B' are perpendicular. Your diagram only has one pair of such lines. You could 'wave' that top line and get any value for φ and wave the bottom line to get any value of θ. If you actually make φ equal to θ then you get your perpendiculars and the theorem is satisfied.

 

[nasu]

It's wrong because your green diagram is not the same as the diagram in the link. Only one of your pairs of sides are perpendicular whereas both pairs of sides are perpendicular in the link diagram. A'C' and AC are perpendicular but also AB and A'B' are perpendicular. Your diagram only has one pair of such lines. You could 'wave' that top line and get any value for φ and wave the bottom line to get any value of θ. If you actually make φ equal to θ then you get your perpendiculars and the theorem is satisfied.

I don't have any green diagram. You may have mixed the posts. I showed the poster of the green diagram the actual theorem. As I showed you too

 

[sophiecentaur]

I don't have any green diagram. You may have mixed the posts. I showed the poster of the green diagram the actual theorem. As I showed you too

Sorry but my issue is with the ‘green’ diagram, posted higher up and which the poster is trying to relate ‘your’ theorem, wrongly. That link you posted is useful and shows he’s not correct. Ah yes - the poster was @simphys

 

[JesseProbst]

Oh dear. Whatever is an angle with a perpendicular side? I'm sure you are referring to something that I learned over sixty years ago but I can't think what it is.

this is when two lines meet, they form right angles.

 

[sophiecentaur]

this is when two lines meet, they form right angles.

Unless you state the whole thing, it’s meaningless. There are two pairs of lines involved. Read that helpful link. It states the actual theorem.

 

[JesseProbst]

Err, ok, thanks, I'll check it

 

[Lnewqban]

...
The problem here is that my geometry bag is very weak, I didn't have any geometry in HS, will fix that sooner or later but anyway.
...

I have found these two websites about Geometry very interesting:
https://www.mathsisfun.com/geometry/index.html

https://www.mathopenref.com/tocs/triangletoc.html

Those are inter-active, and you can play as you learn.