funnyman634
- 2
- 1
When I think of the speed of light being constant for all reference frames, I imagined the scenario in the picture below to exemplify it. Object A is always at rest, object B is moving at half the speed of light along the only given axis, and object C is a light particle moving at the speed of light along the only given axis. The objects are placed at different heights in the image only for visual clarity, so a 1D scenario. The frame on the left is t = 0 (say t is for object A and t' for object B) the objects are all at rest (I know object C can never be at rest if it's a light particle, but then let's just assume it comes into existence the moment the scenario begins). We start the simulation and then freeze it after a second has past, t = 1, the frame on the right. I solve for t' (the amount of time object B felt has passed) based on what has occurred. Why do I get 0.5 seconds and not what the Lorentz factor says I should get, 0.86602540378 seconds ? (1 / gamma or 1 / 1.15470053837925)
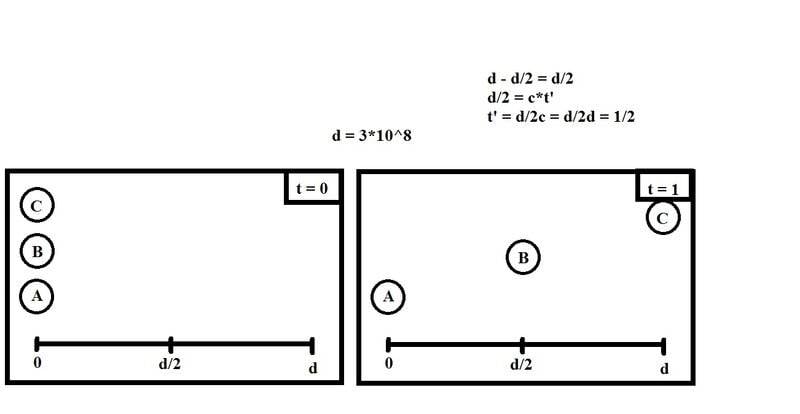
 e makes use of the fact, that B meets x=d/2 at the same time as C meets x=d in A's frame and misses, that these events are not synchronous in B's frame, besides missing the length contraction.
e makes use of the fact, that B meets x=d/2 at the same time as C meets x=d in A's frame and misses, that these events are not synchronous in B's frame, besides missing the length contraction.