##x'=0## and ##t'=0## axes in railcar thought experiment

[zenterix]

TL;DR Summary

In the thought experiment of three moving railcars in a row, the middle one equidistant from the outer two, in which a light ray is emitted from each of the outer two to reach the middle one, how do we reason about the $x'=0$ and $t'=0$ axes in the moving frame of the first railcar?

I am following the book "Special Relativity and Classical Field Theory: The Theoretical Minimum" by Susskind.

I want to go through a sequence of ideas to try to understand simultaneity.

We have a rest frame A and a moving frame B along the x-axis.

Let the coordinates be $x$ and $t$ in frame A and $x'$ and $t'$ in frame B.

Under Newton's laws, we have the transformation from B coordinates to A coordinates as follows

$$t=t'$$

$$x=x'+vt'$$

Here is a depiction of coordinates in frame A

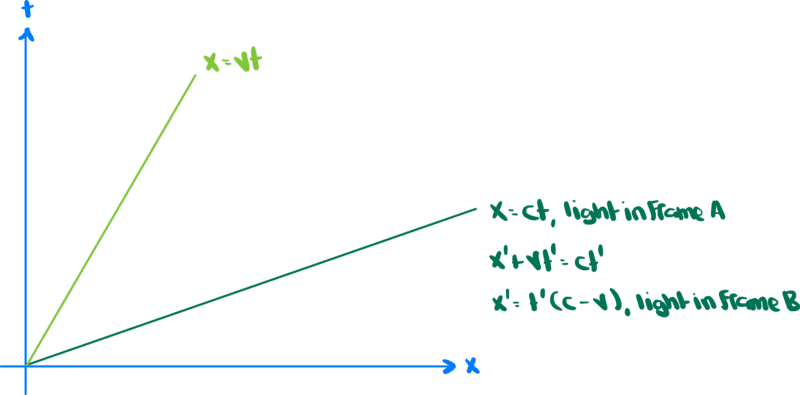
I've drawn in the coordinates of a light ray that is at the origin at $t=0$ (dark green) and the coordinates of frame B if we assume that it too is at the origin at $t=0$ (light green).

Imagine a moving train with three different railcars each separated by a distance of 1. Art, Maggie, and Lenny are each in one of the railcars.

Each of them has an inertial reference frame, though they are simply offset from each other by a fixed distance. We can consider them all to be frame B.

Let's consider frame A our frame.

Let's use relativistic units (meaning that $c=1$ and we can either think about that number as dimensionless or as, e.g. light-seconds per second).

Suppose Art and Lenny both emit a light ray towards Maggie such that the light rays arrive simultaneously at Maggie.

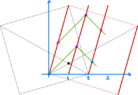
First suppose that the train is not moving. We have the following situation

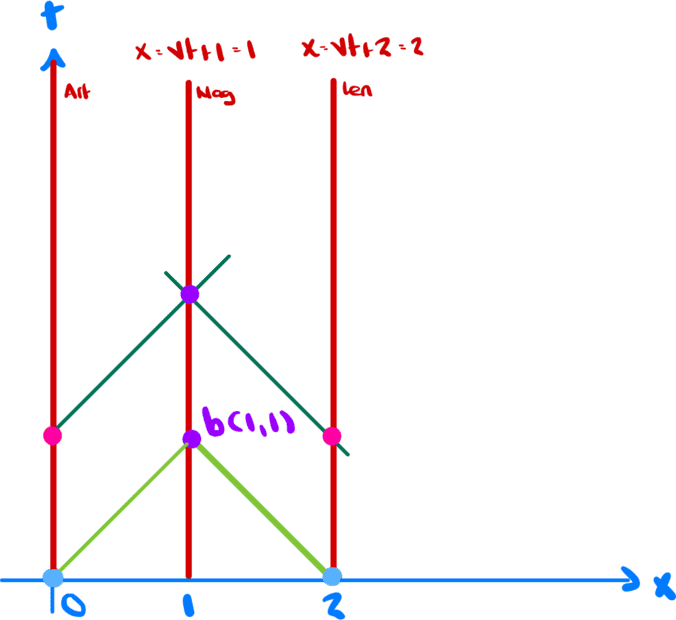
Since $v=0$ we have

$$x=x'$$
$$t=t'$$

Consider the light green lines.

For the one starting at the origin we have

$$x=t$$

The other one satisfies

$$x=-t+t_0$$

Since they meet at $b$, which we know is $(1,1)$ we can easily find the equation

$$x=2-t$$

for the other light green line.

Note that a light ray emitted at $t=t'=0$ from the origin and from $(2,0)$ (in both frames) reaches point $b(1,1)$ simultaneously. The two light blue points are synchronized, as are the two pink points.

In fact, any points on any line $t=t_1$ are synchronized.

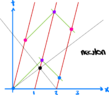
Now consider that the train is moving with speed $v$.

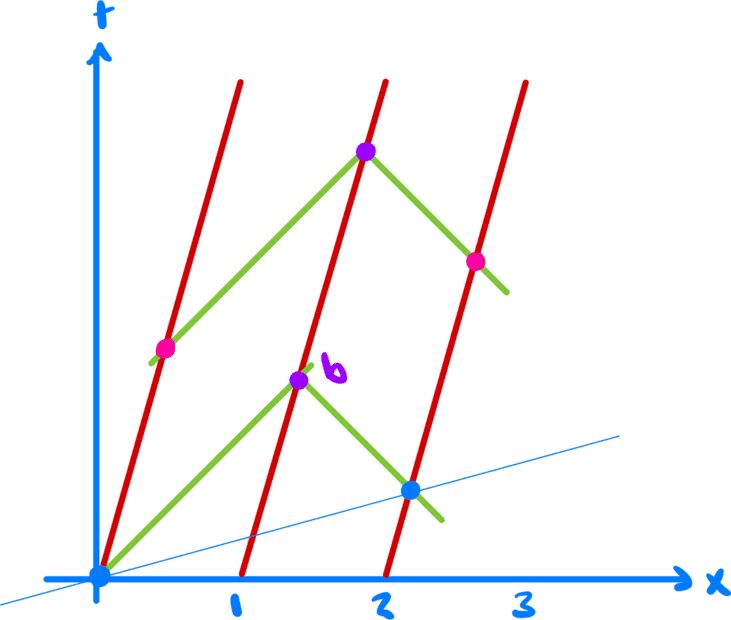
Again, the red lines represent the position in spacetime of the three railcars in frame A.

Assuming that the speed of light is the same in every inertial frame, then we can draw the green lines at 45 degree angles representing emitting light rays from different rail cars. For two light rays to arrive simultaneously at the second rail car at point b, they need to be emitted at the two light blue points (one by Art and one by Lenny).

Notice that in frame A, the times at which they are emitted are no longer the same. The emission of the rays is not synchronized from the point of view of frame A.

Maggie receives both light rays at the same time, and from her frame both Art and Lenny at at the same distance from her so to her the emission of the rays is synchronized. In fact, since the emission by Art occurs at t'=0 then so does the emission by Lenny.

From the point of view of Maggie's frame, all points on the thin blue line are synchronized with each other.

Let's see how Newton would view this situation in graphical terms.

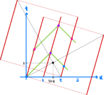
As far as I can tell, we have a situation like

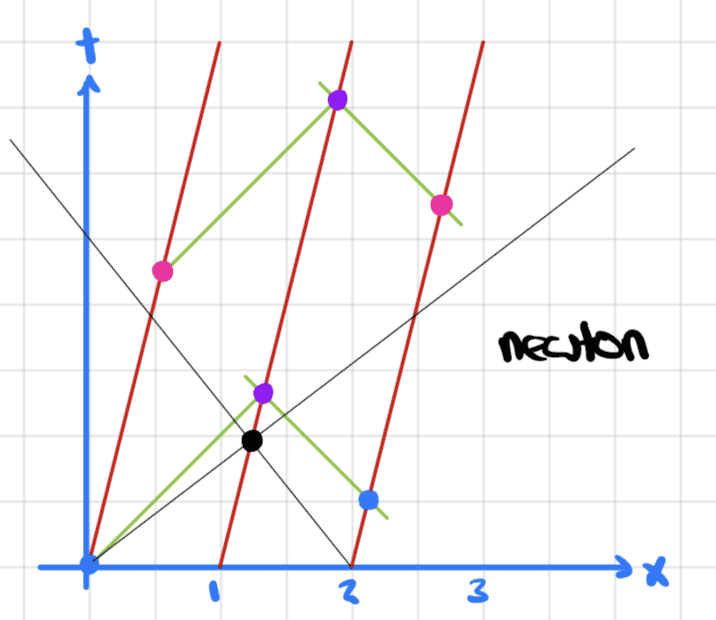
I have drawn the two boxes just to show the symmetry and that in fact the angles are drawn correctly (I think). The point I want to talk about here is the black point.

Notice that I used the gridlines to make the graph precise.

We have here that $c=1$ and $v=\frac{1}{4}$.

The black line starting at the origin represents the light ray emitted by Art from the point of view of frame A

$$x = (c+v)t=(1+v)t=1.25t\tag{1}$$

In Art's frame we have

$$x'=x-vt=(1+v)t-vt=-t\tag{2}$$

In Lenny's frame we have

$$x'=x-vt=(1+v)t-(2+vt)=-2+t\tag{3}$$

Next, consider the black line starting at $(2,0)$ in frame A.

$$x=(-c+v)t+2=(-1+v)t+2=2-0.75t\tag{4}$$

In Art's frame this is

$$x'=(-1+v)t+2-vt=2-t\tag{5}$$

and in Lenny's frame

$$x'=(-1+v)t+2-(2+vt)=-t\tag{6}$$

(1) and (4) are the black lines in the plot.

They meet at

$$(1+v)t=(-1+v)t+2 \implies t=1 \implies x=1+v=1.25$$

In Art's frame we have

$$t=2-t\implies t=1 \implies x'=1$$

And in Lenny's frame we have

$$-2+t=-t\implies t=1\implies x'=-1$$

All of this makes sense mathematically and graphically.

What it means is that under Newton's transformations the origin is synchronous with $(2,0)$ in all frames, which means that a light ray emitted from these two spacetime points reach the equidistant purple point at the same time.

So why is this problematic?

Because measurements of the speed of light in any of the frames shows is constant: $c=1$.

Thus, equations (1) and (4) are incorrect since these equations show a speed of light of 1.25 and 0.75, respectively.

When we make the assumption that the speed of light is constant in every frame, we end up with the green lines in the picture above and now the two blue points are synchronous in the moving frames. They are not synchronous in frame A.

At this point my questions arise.

I'm having a hard time interpreting these results further.

We have Maggie's train car and for light to reach her from the two other equidistant train cars we've seen that the light rays must be emitted at different times in frame A.

From the point of view of Maggie, however, since

1) they arrive at the same time
2) they are equidistant
3) light has a fixed speed
then they have the same time coordinate in her frame. In the case of the blue dots, this time would be $t'=0$. In the case of the pink points, it would be some other time $t_1$.

Finally, there is also the $x'=0$ axis

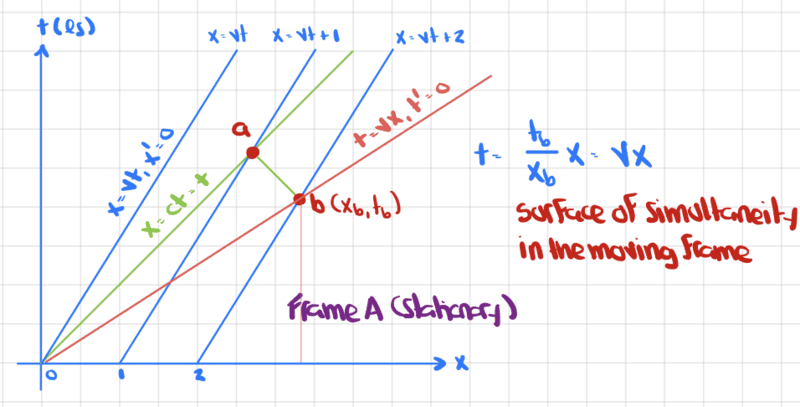
What does it mean that the $x'=0$ axis and the $t'=0$ axis are not at a right angle?

 

[Orodruin]

What does it mean that the x′=0 axis and the t′=0 axis are not at a right angle?

Nothing. The geometry of spacetime is not Euclidean.

Instead, the spacetime geometry is that of Minkowski space, which has a different inner product. With the Minkowski inner product, the $t’$ and $x’$ axes are indeed orthogonal. It just won’t look that way when you draw them on a piece of paper with an inherently Euclidean geometry.

Edit: Note that the $t’$ and $x’$ axes are not orthogonal in the case of the Galilean transform either when drawn in the unprimed system. There it means even less though.

 

[PeterDonis]

Note that the $t’$ and $x’$ axes are not orthogonal in the case of the Galilean transform either when drawn in the unprimed system. There it means even less though.

In Galilean spacetime there isn't even a spacetime metric at all, so there is no well-defined concept of the "angle" between the axes in a spacetime diagram. I assume this is what you are referring to in the last sentence quoted above.

 

[PeroK]

@zenterix there is too much going on in that post. You have multiple spacetime diagrams, different coordinate systems and a complicated attempt to analyse the relativity of simultaneity.

IMO, there's too much to digest there until you are more familiar with SR.

Personally, I think that spacetime diagrams are trickier than you might expect. All our native geometric intuition is Euclidean. And that intuition needs to be unlearned before they make much sense.

 

[Dale]

In Galilean spacetime there isn't even a spacetime metric at all, so there is no well-defined concept of the "angle" between the axes in a spacetime diagram. I assume this is what you are referring to in the last sentence quoted above.

Yes, but in terms of the metric they are orthogonal. So the question about them not being orthogonal is just about the diagram. Hence, @Orodruin’s comment.

 

[PeterDonis]

in terms of the metric they are orthogonal

In terms of what metric? As I said, there isn't a spacetime metric at all in Galilean spacetime. So there is no way of even computing an inner product between the time and space axes.

 

[Dale]

In terms of what metric? As I said, there isn't a spacetime metric at all in Galilean spacetime. So there is no way of even computing an inner product between the time and space axes.

The Minkowski metric. The question was about the Minkowski spacetime diagram. The axes are orthogonal in that metric but not perpendicular on the corresponding diagram. So the question is about the diagram and not the metric. Hence @Orodruin is correct to point out that it isn’t orthogonal on the corresponding Galilean diagram either. The fact that there is no corresponding Galilean spacetime metric is not relevant because the question is about the diagram not the metric.

 

[PeterDonis]

The Minkowski metric.

The comment by @Orodruin that I responded to was about Galilean spacetime, not Minkowski spacetime. I agree that in Minkowski spacetime the time and space axes of any inertial frame are orthogonal.

the question is about the diagram not the metric

The exact comment by @Orodruin that I responded to was "There [i.e., in Galilean spacetime] it [i.e., how the axes look in the diagram] means even less, though." That comment was not just about the diagram. (Or, if I am misreading the comment somehow, I would like @Orodruin to clarify what it means. I said in post #3 that I was making an assumption about what it meant.)

 

[zenterix]

@zenterix there is too much going on in that post. You have multiple spacetime diagrams, different coordinate systems and a complicated attempt to analyse the relativity of simultaneity.

IMO, there's too much to digest there until you are more familiar with SR.

Personally, I think that spacetime diagrams are trickier than you might expect. All our native geometric intuition is Euclidean. And that intuition needs to be unlearned before they make much sense.

The thing is, everything going on in my post is the derivation (mathematical and graphical) in the first thirty pages of the book I'm reading.

I didn't try to go off on any tangent or anything. With the exception of the part about Newton everything is in the book.

The post may be long but that is simply because I tried to be thorough with regard to each step in the reasoning. There are two frames and everything is shown in the final picture.

Now, perhaps you may say the book itself it too simplistic?

One way or the other, you are right that I need to become more familiar with SR and so I will keep going.

 

[PeroK]

The thing is, everything going on in my post is the derivation (mathematical and graphical) in the first thirty pages of the book I'm reading.

It doesn't take 30 pages to introduce the relativity of simultaneity.

Now, perhaps you may say the book itself it too simplistic?

it seems too complicated. One wagon would do.

One way or the other, you are right that I need to become more familiar with SR and so I will keep going.

I meant you should tackle one thing at a time.

Do you understand the relativity of simultaneity?

 

[PeroK]

For a simple analysis see this, for axample:

https://www.physicsforums.com/threa...-the-relativity-of-again.1055347/post-6928164

 

[zenterix]

It doesn't take 30 pages to introduce the relativity of simultaneity.

it seems too complicated. One wagon would do.

I meant you should tackle one thing at a time.

Do you understand the relativity of simultaneity?

Usually I write prequels to my question to show my general level of understanding of a concept or topic. I think everything about my post has to do with simultaneity. I'm not sure what the other things are that you say I am trying to tackle.

The term "relativity of simultaneity" itself hasn't come up yet in this book.

That being said, I would imagine that it means that simultaneity (which is a term that I haven't seen an exact definition for yet and which I think of currently as meaning occurring at the same time in a certain reference frame) depends on the inertial reference frame.

Simultaneity in my understanding is a relationship between certain events, and that relationship depends on the reference frame. In the context of my post, the events are emissions of light rays. I believe the pictures I drew and the equations I wrote show that under Einstein's assumption of the speed of light being the same in every frame, we have two events that are simultaneous in a moving frame and not simultaneous in a stationary frame.

 

[Nugatory]

Simultaneity in my understanding is a relationship between certain events, and that relationship depends on the reference frame.

The relationship between events (spacelike-separated, timelike-separated, lightlike-separated) is the same no matter what frame we use.

Simultaneity is a relationship between the coordinates we choose to label events: two events are simultaneous if they have the same time coordinate. That of course will depend on the reference frame.

 

[zenterix]

The relationship between events (spacelike-separated, timelike-separated, lightlike-separated) is the same no matter what frame we use.

Simultaneity is a relationship between the coordinates we choose to label events: two events are simultaneous if they have the same time coordinate. That of course will depend on the reference frame.

One thing I have doubts about is the following, in the context of the three railcars. Consider the following picture

In this picture the third railcar is at a further distance from the middle railcar. As one would expect, the farther away the third railcar is the sooner the light ray has to be emitted from that railcar to reach the light ray emitted from the first ray car.

But then, in the moving frame, is point $b$ above simultaneous with the whole orange line that we had previously determined was the $t'=0$ line?

In fact, are all points on the line passing through $a$ and $b$ simultaneous all the points on the orange line?

Now, I think the answer is no but I can't express exactly why.

I think it has to do with the fact that it is know that the distance between the first railcar and the middle railcar, and between the third railcar and the middle railcar is different.

I guess I don't understand how distance is baked into the notion of simultaneity.

 

[Nugatory]

I guess I don't understand how distance is baked into the notion of simultaneity.

First let's look at how simultaneity is represented on a Minkowski diagrams: Draw a straight line through two events. If that line is parallel to the x-axis of a given frame then those two events and all other events on that line are simultaneous in that frame. This makes sense when you consider that a line parallel to the x-axis is a line of constant $t$, which in turn follows from the fact that the x and t axes of a frame are orthogonal in the Minkowski geometry even if the don't look that way on a Euclidean sheet of paper.

 

[PeroK]

The term "relativity of simultaneity" itself hasn't come up yet in this book.

I thought the whole purpose of your post was to show that simultaneity is relative, I.e. frame dependent? I can't believe Susskind uses a different term.

That being said, I would imagine that it means that simultaneity (which is a term that I haven't seen an exact definition for yet and which I think of currently as meaning occurring at the same time in a certain reference frame) depends on the inertial reference frame.

Yes, exactly.

Simultaneity in my understanding is a relationship between certain events, and that relationship depends on the reference frame. In the context of my post, the events are emissions of light rays. I believe the pictures I drew and the equations I wrote show that under Einstein's assumption of the speed of light being the same in every frame, we have two events that are simultaneous in a moving frame and not simultaneous in a stationary frame.

Yes, exactly. But, there are simpler ways to demonstrate this. Which was my point.

My other point was that some people promote the idea of using Minkowski spacetime diagrams as the best way to get to with grips with SR initially. I'm not convinced. Personally, they were the hardest thing for me to understand when I first learned SR.

You have to decide for yourself to what extent to rely on them at this stage.

 

[PeroK]

That said, that the line of constant $t'$ is not a line of constant $t$ is pretty much the relativity of simultaneity in a nutshell. You don't really need railcars and light signals. It's inherent in a Minkowski diagram for two reference frames.

 

[Orodruin]

In Galilean spacetime there isn't even a spacetime metric at all, so there is no well-defined concept of the "angle" between the axes in a spacetime diagram. I assume this is what you are referring to in the last sentence quoted above.

Exactly. Without a metric ”orthogonal” is meaningless. However, just as for the Minkowski case, some axes will not be orthogonal with respect to the Euclidean metric of the paper they are drawn on - which in itself has no physical meaning.

 

[Sagittarius A-Star]

You don't really need railcars and light signals. It's inherent in a Minkowski diagram for two reference frames.

Susskind makes it so complex in his book, because he does not simply present and use the Minkowski diagram. He derives it directly from the two postulates and uses a geometrical construction on the paper to find the x' axis. After that, he derives the Lorentz transformation in an easy way from the Minkowski diagram.

The most used derivation path in textbooks is:

• Two postulates -> LT -> Minkowski diagram.

Susskind does:

• Two postulates -> Minkowski diagram -> LT.

 

[PeroK]

Susskind makes it so complex in his book, because he does not simply present and use the Minkowski diagram. He derives it directly from the two postulates and uses a geometrical construction on the paper to find the x' axis. After that, he derives the Lorentz transformation in an easy way from the Minkowski diagram.

The most used derivation path in textbooks is:

• Two postulates -> LT -> Minkowski diagram.

Susskind does:

• Two postulates -> Minkowski diagram -> LT.

That explains things. Thanks. That sounds like a useful pedagogic test whether students really do understand things better geometrically. I have my doubts when it comes to Minkowski spacetime.

 

[Orodruin]

That explains things. Thanks. That sounds like a useful pedagogic test whether students really do understand things better geometrically. I have my doubts when it comes to Minkowski spacetime.

For some time I have started my SR lectures by taking a couple of lectures to talk about Euclidean geometry and directly lifting the concepts to Minkowski space (after discussing why Minkowski space is a good idea and keeping mindful of how the sign in the metric spices things up). However, I would not base the LT derivation on diagramatical considerations. Rather deriving it first in the cosh-sinh form in analogy to Euclidean rotations. Works like a charm.

Note: I would probably not take this approach at a very introductory level. My course is a 4th year specialization course, not the tipical intro/modern physics one.

 

[Dale]

some people promote the idea of using Minkowski spacetime diagrams as the best way to get to with grips with SR initially. I'm not convinced. Personally, they were the hardest thing for me to understand when I first learned SR

For me, they were indispensable. I had started with a textbook that took a no-spacetime approach. It was pure algebra and thought experiments. I had some serious misconceptions for 7 years. And then I just randomly stumbled onto spacetime diagrams online. I drew one spacetime diagram on my own and everything suddenly clicked.

I think that there is no pedagogical “one ring to rule them all”. Different students will need different presentations.

 

[zenterix]

That said, that the line of constant $t'$ is not a line of constant $t$ is pretty much the relativity of simultaneity in a nutshell. You don't really need railcars and light signals. It's inherent in a Minkowski diagram for two reference frames.

Sure I'll bet you don't need railcars, but isn't this whole approach akin or analogous to learning about the derivative for the first time? You can learn about it in terms of a function f(x) and the concept of the limit of a specific mathematical expression.

I think you add something by thinking about it in terms of moving objects or vehicles with displacement, velocity, and acceleration. You don't need these things, but they can provide a nice perspective for thinking about the concepts in a less abstract way.

Hence, the railcars, no?

 

[zenterix]

I've asked questions about SR before. I was reading French and Resnick and the suggestion was that these books might be pedagogically outdated. I will continue reading those but I also switched to Susskind and Tsamparlis.

I will read them all. When you guys talk about approaches different to Susskind, what books are you referring to?

 

[PeroK]

Sure I'll bet you don't need railcars, but isn't this whole approach akin or analogous to learning about the derivative for the first time? You can learn about it in terms of a function f(x) and the concept of the limit of a specific mathematical expression.

I think you add something by thinking about it in terms of moving objects or vehicles with displacement, velocity, and acceleration. You don't need these things, but they can provide a nice perspective for thinking about the concepts in a less abstract way.

Hence, the railcars, no?

I don't see the analogy with calculus. SR ultimately boils down to events and the coordinates of those events in different reference frames. The more elaborate the scenario, the more the fundamentals may get lost.

In terms of books, the first chapter of Morin is free online.

https://scholar.harvard.edu/david-morin/special-relativity

That said, it's a big decision to abandon one book and move to another. If you understand what Susskind is doing, then perhaps you ought to give him a chance.

 

[Dale]

I've asked questions about SR before. I was reading French and Resnick and the suggestion was that these books might be pedagogically outdated. I will continue reading those but I also switched to Susskind and Tsamparlis.

I will read them all. When you guys talk about approaches different to Susskind, what books are you referring to?

Personally, I really like Susskind's approach.