Can Light Rays Cross Near a BH? - Simulated w/ Matlab

[Haorong Wu]

TL;DR

When I simulate that two parallel light rays pass near a Kerr BH, the result shows that they cross each other. Is it possible?

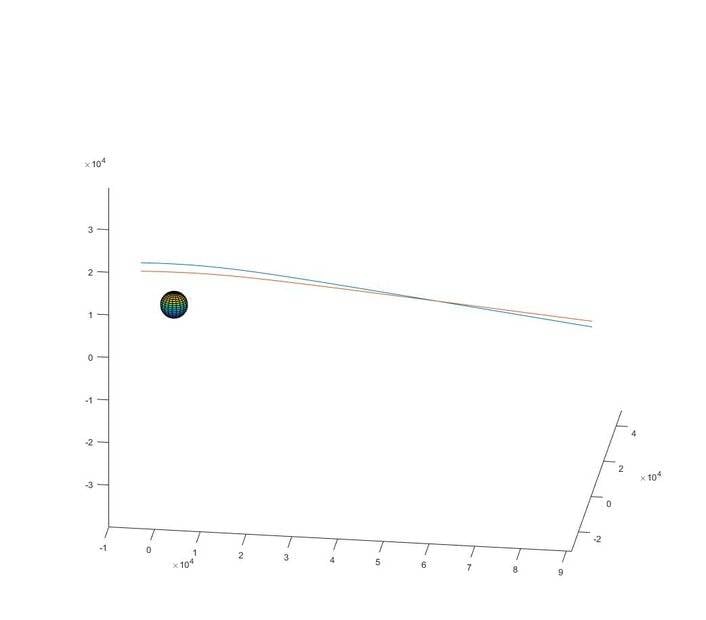
Hi. I use Matlab to simulate that two parallel light rays pass near a Kerr BH. The angular momentum of the BH points to the $z$ direction. The $z$ components of the start points of the two rays are $1\times 10^3 ~\rm{m}$ and $- 1\times 10^3 ~\rm{m}$, respectively. The result, as shown in the figure, indicates that the rays cross each other. In the end, the $z$ components of the two rays are $-667~\rm{m}$ and $667~\rm{m}$, respectively.

I am not sure if this is possible or not. Maybe there are some errors in my model. How can I check if my result is correct or not?

Thanks.

 

[Ibix]

You haven't really explained your initial conditions, so it's hard to comment. I think your rays start symmetrically above and below the equatorial plane. What are their initial directions, and what are the mass and angular momentum parameters of the hole?

 

[Haorong Wu]

@Ibix

Sorry, I thought that is not important, so I did not mention it. Here are the parameters (all are in Cartesian coordinates):

mass of BH is $1.988\times10^{30}~\rm{kg}=1.47\times10^3~\rm{m}$ ;
angular momentum per unit mass is $0.9$ (along z-axis);
position of BH is $(0,~0,~0)$;
initial positions of rays are $(-1\times 10^4,~2\times 10^4,~1\times 10^3)$ and $(-1\times 10^4,~2\times 10^4,~-1\times 10^3)$, respectively;
both initial wave vectors are $(1.03\times 10^7 ,~1.82\times 10^6 , ~ 0)$;

The results are:
the final positions of rays are $(9.12\times 10^4,~1.55\times 10^3,~-667)$ and $(9.12\times 10^4,~1.55\times 10^3,~667)$, respectively;
the final wave vectors are $(1.05\times 10^7,~-2.28\times 10^6,~-1.90\times 10^5)$ and $(1.05\times 10^7,~-2.28\times 10^6,~1.90\times 10^5)$, respectively.

The wave number is increased by $2.36\times10^5~\rm{m^{-1}}$, but I think that is due to the calculation error of the ode45 algorithm.

 

[Dale]

This is gravitational lensing.