Can Relativity Explain the Confusion of the Twins Paradox?

[M1keh]

In each observer's own rest frame, their speed is 0.
Both will agree on their distance traveled relative to the road in an hour, in Newtonian physics. But that's just a particular feature of Newtonian physics where all rulers and clocks agree, it's not in general true that if "the laws of physics agree", then observers in different frames must agree on the distance A moves relative to B in a given amount of time. The laws of physics agreeing just means the same equations are used in every frame to calculate things, that's all. Yes, as a general rule, the distances can only be equal in one frame. But this is no different from the fact that in Newtonian physics two objects traveling in opposite directions can have equal speeds in only one frame.

Whilst that's true, it's now what I was saying ? In Newtonian Physics both objects would measure the other's speed as exactly the same (assuming they measure themselves as stationery). Therefore the rules are the same ?

Also, note that if the distances are the same in the rest frame of each group of clocks, then they will view each other symmetrically--if they're both 6 ly apart in their own rest frames, then each will observe the other group to be 4.8 ly apart. What do you mean, "before they're all sync'd in B's f.o.r."? In the frame where the B's are at rest before reaching the As and accelerating, they are all in sync throughout the process. For example, when B1 has time t=-2 years (t=0 years is defined as the time the B's reach the A's), B2 also has time t=-2 years according to this frame's definition of simultaneity, as does B3.

Ok. Let's try to clear this one up. It may be I misunderstood the earlier discussions.

If A's are 6ly apart, B's are traveling at 0.6c relative to A's, therefore their measure of the distance must be 4.8ly, (using $$1 / \sqrt{1 - v^2/c^2}$$ ).

Is this one of the 'rules of physics' that we're using or did I misread it ?

All of the earlier examples were specified on this basis ? I earlier suggested that both should be 6ly and measure the other as 4.8ly but everyone said this was incorrect ?

( Must stop typing so many ? )

Yes, B3 passes A1 before any of the others pass each other. Wait, you're changing the scenario now, you never said anything about the B's adjusting the times on their clocks before. All my and jtbell's previous explanations were based on the assumption that everyone is letting their clocks run naturally after the 3 Bs are synchronized in their rest frame and the three As are synchronized in theirs. Also, it was assumed that the Bs read t=0 at the moment each reaches their own corresponding A (ie when B3 reaches A3 and so forth, not when B3 reaches A1), and A1 also reads 0 when B1 reaches it, although if the three As are synchronized in their own rest frame then A2 and A3 won't read 0 when their own corresponding Bs reach them.

Apologies. Yes I changed it. The example seemed to have been reduce into a snapshot of time when the B's see themselves as level with the A's.

This restricts the example somewhat.

I didn't think there'd be a problem with syncing watches at the first event and then playing the events forward ?

Would you like to change the scenario now, or were you not understanding that this was what jtbell and I had been assuming? Sync them in whose frame, the rest frame of the three Bs (before they accelerate to stop relative to the As, if you're still assuming that) or the rest frame of the As? Only if one of the two sets of clocks have been set so that they are out-of-sync in their own rest frame. Under the original assumption I described above, or making some new assumptions about the B clocks being reset when B3 passes A1? If the latter you need to be clear about what frame you want the Bs to be synchronized in.

Interesting question.

If A1 & B3 are passing each other. They can sync their times across f.o.r's ? A simultaneous event ?

Presumably there's no question that the A's can then sync their times effectively instantaneously, in their local f.o.r, as can the B's ? I agree that by the time the B's sync their watches locally, they'd be out of sync with the A's but they would have, effectively, been in sync when A1 & B3 passed ?


I may have confused the conversation. Maybe it's worth listing out the rules we're working to ? Which of these are correct and which are not ?

* Time dilation is a factor of relative speed, which at 0.6c is 0.8.

* Length contraction is, effectively, the inverse of time dilation, 1.25.

* At 0.6c, a local observer must expect the remote observer to measure time at 0.8 of his time.

* At 0.6c, a local observer must expect the remote observer to measure distance at 0.8 of his distance.

* Time dilation is a function of relative speed, not relative velocity.

* Two passing observers can agree on the 'simultaneous event' of them passing each other ( & can therefore sync watches at that point ).

Now, I'm not sure how you specify the length between observer's function that you listed earlier. How would you put that into words ?


Thanks.

 

[JesseM]

Whilst that's true, it's now what I was saying ? In Newtonian Physics both objects would measure the other's speed as exactly the same (assuming they measure themselves as stationery). Therefore the rules are the same ?

Yes, their view of each other's speed is symmetrical.

Ok. Let's try to clear this one up. It may be I misunderstood the earlier discussions.

If A's are 6ly apart, B's are traveling at 0.6c relative to A's, therefore their measure of the distance must be 4.8ly, (using $$1 / \sqrt{1 - v^2/c^2}$$ ).

Is this one of the 'rules of physics' that we're using or did I misread it ?

The length contraction factor of $$1 / \sqrt{1 - v^2/c^2}$$ is a general equation that holds in all inertial frames. But this equation tells you the amount that the length is contracted from the length in the rest frame--and since the A clocks and B clocks have different separations in their rest frames, then the separation each measures the other ones to have will also be different. The A clocks are 6 ly apart in their own rest frame and therefore 4.8 ly apart in the B frame, while the B clocks are 4.8 ly apart in their own rest frame and therefore 3.84 ly apart in the A frame. So applying the same laws of physics in both frames results in each getting a different result for the other's separation, since their separation in their own rest frames is different.

All of the earlier examples were specified on this basis ? I earlier suggested that both should be 6ly and measure the other as 4.8ly but everyone said this was incorrect ?

Yes, it's incorrect. In the A frame, the B clocks are 3.84 ly apart.

Apologies. Yes I changed it. The example seemed to have been reduce into a snapshot of time when the B's see themselves as level with the A's.

This restricts the example somewhat.

I didn't think there'd be a problem with syncing watches at the first event and then playing the events forward ?

I'm fine with changing the scenario, but you still haven't explained what you mean by "syncing watches". In which frame do the three B clocks synchronize their watches?

Under the original assumption I described above, or making some new assumptions about the B clocks being reset when B3 passes A1? If the latter you need to be clear about what frame you want the Bs to be synchronized in.

Interesting question.

If A1 & B3 are passing each other. They can sync their times across f.o.r's ? A simultaneous event ?

At the moment A1 and B3 pass each other, if they each set their clock to read 0, then it will be true in all frames that they both read 0 at the same moment, since this is an event which happens at a single location. But that's not what I was asking. I was asking what the other two B clocks, B1 and B2, are doing--if you want B1 and B2 to also set themselves to 0 "at the same time" that B3 passes A1, you need to specify which frame's definition of simultaneity they should use, since if B1 and B2 set themselves to read 0 simultaneously with B3 passing A1 in one frame, in other frames they will set themselves to read zero earlier than or later than the moment B3 passes A1.

Presumably there's no question that the A's can then sync their times effectively instantaneously, in their local f.o.r, as can the B's ?

I don't understand your question here--what is a "local f.o.r.", for example? "Local" in relativity usually refers to events that happen at a single place and time like two clocks passing arbitrarily close to each other, while a frame of reference is a system of coordinates covering a large region of space and time, and giving a definition of simultaneity for distant (i.e. not local) events.

And what does it mean for the A's to sync their times effectively instantaneously? Sync their times with what, each other (in which case you need to pick one frame's definition of simultaneity) or with a B that's passing them (in which case, if you say that A1 sets itself to the same time as B3 at the moment they pass, you need to specify which Bs the other two As set themselves to match the time of as they pass) or something else?

I agree that by the time the B's sync their watches locally

What does sync their watches locally mean? Sync with what? Can you be explicit about what event triggers each of the Bs--B1, B2, and B3--to reset their watch, and if it's a distant event (like B2 setting its watch to 0 at the 'same time' that B3 passes A1) then specify which frame's definition of simultaneity you're using? Without these specifics I can't really follow your way of talking here.

I may have confused the conversation. Maybe it's worth listing out the rules we're working to ? Which of these are correct and which are not ?

* Time dilation is a factor of relative speed, which at 0.6c is 0.8.

* Length contraction is, effectively, the inverse of time dilation, 1.25.

Yes.

* At 0.6c, a local observer must expect the remote observer to measure time at 0.8 of his time.

Again, I don't understand how you're using the word "local" here. Do you just mean that if I see a clock moving at 0.6c in my own rest frame, I will measure it to tick at 0.8 the rate of my own clocks? If so, then that's correct.

* At 0.6c, a local observer must expect the remote observer to measure distance at 0.8 of his distance.

Again, if you just mean that a ruler moving at 0.6c in my frame will be measured to be shrunk to 0.8 the size of my ruler in my frame, then yes.

* Time dilation is a function of relative speed, not relative velocity.

Yes.

* Two passing observers can agree on the 'simultaneous event' of them passing each other ( & can therefore sync watches at that point ).

I would use the word "local" for these events, since there is a negligible spatial separation between them. "Simultaneous events" can mean events that happen at a large distance from each other and are simultaneous in one particular reference frame. Of course, local events will be simultaneous in every reference frame, they'll be no disagreement about what each clock read at the moment they passed next to each other.

Now, I'm not sure how you specify the length between observer's function that you listed earlier. How would you put that into words ?

What do you mean by "the length between observer's function"? Can you quote from the post where I gave this function so I'll know what you're referring to?

 

[M1keh]

Apolgies. My post wasn't clear and I'm struggling with some of the terminology and where it applies.

Yes, their view of each other's speed is symmetrical. The length contraction factor of $$1 / \sqrt{1 - v^2/c^2}$$ is a general equation that holds in all inertial frames. But this equation tells you the amount that the length is contracted from the length in the rest frame--and since the A clocks and B clocks have different separations in their rest frames, then the separation each measures the other ones to have will also be different. The A clocks are 6 ly apart in their own rest frame and therefore 4.8 ly apart in the B frame, while the B clocks are 4.8 ly apart in their own rest frame and therefore 3.84 ly apart in the A frame.

I'm struggling with this. The formula is 'symmetrical' in both f.o.r's, but it's use or the interpretation of the results isn't ?

If you look from A's f.o.r, we start with A measures the distance as 6ly. We apply the formula and say, therefore B must see the distance as 4.8ly. Then we jump to B's f.o.r and say 'B MUST therefore measure the distance as 4.8 ly'.

But if you then apply this from B's f.o.r, we start with B measures the distance as 4.8ly. We apply the formula and say, therefore A must see the distance as 3.84 ly, but when we jump back to A's f.o.r, it isn't.

Now if the rules apply equally well from both f.o.r's, why do we get two different results from applying the rules ? Bearing in mind, we could just as easily have started from B's f.o.r and set the initial rules from there ?

So applying the same laws of physics in both frames results in each getting a different result for the other's separation, since their separation in their own rest frames is different. Yes, it's incorrect. In the A frame, the B clocks are 3.84 ly apart. I'm fine with changing the scenario, but you still haven't explained what you mean by "syncing watches". In which frame do the three B clocks synchronize their watches?

By local, I meant local to their own f.o.r. So the B's can instantaneously synchronise their watches to the event where B3 passes A1, as can the A's ?

At the moment A1 and B3 pass each other, if they each set their clock to read 0, then it will be true in all frames that they both read 0 at the same moment, since this is an event which happens at a single location.

Ok.

But that's not what I was asking. I was asking what the other two B clocks, B1 and B2, are doing--if you want B1 and B2 to also set themselves to 0 "at the same time" that B3 passes A1, you need to specify which frame's definition of simultaneity they should use, since if B1 and B2 set themselves to read 0 simultaneously with B3 passing A1 in one frame, in other frames they will set themselves to read zero earlier than or later than the moment B3 passes A1.

?? If the B's can observe B3 passing A1 and the A's can observe A1 passing B3. If they all synchroise their watches to the time this event happens in their own f.o.r, at the instant that they observed the event, don't they all agree on the exact time their watches show when the event happened ??

If the A1 synchs with B3 and then the A's synch their watches with A1 in their f.o.r and the B's synch their watches with B3 in their f.o.r, aren't all of the watches synch'd to each other in both f.o.r's at that moment, but then the times on A's and B's watches drift apart afterwards ?

I don't understand your question here--what is a "local f.o.r.", for example? "Local" in relativity usually refers to events that happen at a single place and time like two clocks passing arbitrarily close to each other, while a frame of reference is a system of coordinates covering a large region of space and time, and giving a definition of simultaneity for distant (i.e. not local) events.

So 'locally' means at the same time & place and 'simultaneously' means a single event viewed from our super-human viewing point, but potentially viewed as happening at different times from different f.o.r's ?

Is there a term for a single event witnessed within a single f.o.r by multiple observers at different places, ie. All the B's viewing B3 pass by A1 ? An f.o.r-local event ?

And what does it mean for the A's to sync their times effectively instantaneously? Sync their times with what, each other (in which case you need to pick one frame's definition of simultaneity) or with a B that's passing them (in which case, if you say that A1 sets itself to the same time as B3 at the moment they pass, you need to specify which Bs the other two As set themselves to match the time of as they pass) or something else? What does sync their watches locally mean? Sync with what? Can you be explicit about what event triggers each of the Bs--B1, B2, and B3--to reset their watch, and if it's a distant event (like B2 setting its watch to 0 at the 'same time' that B3 passes A1) then specify which frame's definition of simultaneity you're using? Without these specifics I can't really follow your way of talking here.

Again, apologies. All 6 sync their watches to when they observe A1 & B3 pass each other. As the event is local to A1 & B3 it's also a common event for A2, A3, B2 & B3 ? The A's will all agree on an event in their f.o.r and the B's will all agree on an event in their f.o.r ?

Yes. Again, I don't understand how you're using the word "local" here. Do you just mean that if I see a clock moving at 0.6c in my own rest frame, I will measure it to tick at 0.8 the rate of my own clocks? If so, then that's correct. Again, if you just mean that a ruler moving at 0.6c in my frame will be measured to be shrunk to 0.8 the size of my ruler in my frame, then yes. Yes. I would use the word "local" for these events, since there is a negligible spatial separation between them. "Simultaneous events" can mean events that happen at a large distance from each other and are simultaneous in one particular reference frame. Of course, local events will be simultaneous in every reference frame, they'll be no disagreement about what each clock read at the moment they passed next to each other. What do you mean by "the length between observer's function"? Can you quote from the post where I gave this function so I'll know what you're referring to?

Lets ignore that last bit for now. It doesn't help. It'll come back later.

Are the rules :

* Time dilation @ 0.6c = 0.8.
* Length contraction @ 0.6c = 1.25
* 'Local' events are events happening at the same point in space and are viewed as happening simultaneously by anyone at that point in space, in all f.o.r's.
* Simultaneous events are events that happen at the same time but may be viewed as happening at different times from different f.o.r's ?

* All observers within a single f.o.r will observe an event happening at the same time. (f.o.r-local event ?).

* All rules must work the same in any f.o.r.

 

[jtbell]

If you look from A's f.o.r, we start with A measures the distance as 6ly.

I assume you mean the distance between, say, clocks A1 and A2 in our example.

We apply the formula and say, therefore B must see the distance as 4.8ly. Then we jump to B's f.o.r and say 'B MUST therefore measure the distance as 4.8 ly'.

Right.

But if you then apply this from B's f.o.r, we start with B measures the distance as 4.8ly. We apply the formula and say, therefore A must see the distance as 3.84 ly, but when we jump back to A's f.o.r, it isn't.

If you're still referring to clocks A1 and A2, we cannot apply the length contraction formula in the same way here, to switch from frame B back to frame A, because A1 and A2 are moving in frame B.

However, we can apply the length contraction formula to the distance between clocks B1 and B2 in our example, to switch from frame B back to frame A, because B1 and B2 are at rest in frame B.

Explanation: in the length contraction formula

$$L = L_0 \sqrt {1 - v^2 / c^2}$$

$L_0$ is always the length of an object, or the distance between two objects at rest with respect to each other, in the reference frame in which the objects are at rest. We often call this the proper length of the object.

In the example we're discussing here, the distance between clocks A1 and A2, as measured in frame B, is not the proper length between A1 and A2, because A1 and A2 are not at rest in frame B. Therefore we cannot use it as $L_0$ in the length contraction formula, in switching from frame B to frame A.

On the other hand, the distance between B1 and B2, as measured in frame B, is the proper length between B1 and B2, because B1 and B2 are at rest in frame B. Therefore we can use it as $L_0$ in the length contraction formula, in switching from frame B to frame A.

 

[M1keh]

I assume you mean the distance between, say, clocks A1 and A2 in our example.



Right.



If you're still referring to clocks A1 and A2, we cannot apply the length contraction formula in the same way here, to switch from frame B back to frame A, because A1 and A2 are moving in frame B.

However, we can apply the length contraction formula to the distance between clocks B1 and B2 in our example, to switch from frame B back to frame A, because B1 and B2 are at rest in frame B.

Explanation: in the length contraction formula

$$L = L_0 \sqrt {1 - v^2 / c^2}$$

$L_0$ is always the length of an object, or the distance between two objects at rest with respect to each other, in the reference frame in which the objects are at rest. We often call this the proper length of the object.

In the example we're discussing here, the distance between clocks A1 and A2, as measured in frame B, is not the proper length between A1 and A2, because A1 and A2 are not at rest in frame B. Therefore we cannot use it as $L_0$ in the length contraction formula, in switching from frame B to frame A.

On the other hand, the distance between B1 and B2, as measured in frame B, is the proper length between B1 and B2, because B1 and B2 are at rest in frame B. Therefore we can use it as $L_0$ in the length contraction formula, in switching from frame B to frame A.

Hold on. That's a new 'rule'. Not seen that one before.

We can't use length contraction for B's measurement of the distance between A1 and A2, because they're moving relative to B ?

If A measures the distance between two objects as 6ly whether or not they're moving in his f.o.r, presumably B, moving at 0.6c relative to A will measure the distance between the objects as 4.8 ly, whether or not they are moving ?

The length contraction is a function of the difference in speed between A & B, not the speed of the objects ?

 

[jtbell]

If A measures the distance between two objects as 6ly whether or not they're moving in his f.o.r, presumably B, moving at 0.6c relative to A will measure the distance between the objects as 4.8 ly, whether or not they are moving?

No. B will measure the distance between the objects as 4.8 ly, only if the objects are at rest in A's reference frame. Only then is $L_0$, the proper distance between the objects, equal to 6 ly (the distance that A measures).

 

[JesseM]

I'm struggling with this. The formula is 'symmetrical' in both f.o.r's, but it's use or the interpretation of the results isn't ?

If you look from A's f.o.r, we start with A measures the distance as 6ly. We apply the formula and say, therefore B must see the distance as 4.8ly. Then we jump to B's f.o.r and say 'B MUST therefore measure the distance as 4.8 ly'.

But if you then apply this from B's f.o.r, we start with B measures the distance as 4.8ly. We apply the formula and say, therefore A must see the distance as 3.84 ly, but when we jump back to A's f.o.r, it isn't.

As jtbell said, it is understood that the lorentz contraction formula tells you how much a ruler's length will be shrunk from its length in its own rest frame. Now, you could come up with a general formula that tells you "if an object's length in your frame is L and its speed in your frame is v1, what is its length in a frame which is moving at speed v2 in the same/the opposite direction", and this formula would work the same way in every frame, but the lorentz contraction formula is not it.

By local, I meant local to their own f.o.r. So the B's can instantaneously synchronise their watches to the event where B3 passes A1, as can the A's ?

OK, as I said that isn't the way "local" is used in relativity, but I think I understand what you're saying now. In the B rest frame, B1 and B2 will read 0 at the same time B3 passes A1, and in the A rest frame, A2 and A3 will read 0 at the same time B3 passes A1, is that correct?

But that's not what I was asking. I was asking what the other two B clocks, B1 and B2, are doing--if you want B1 and B2 to also set themselves to 0 "at the same time" that B3 passes A1, you need to specify which frame's definition of simultaneity they should use, since if B1 and B2 set themselves to read 0 simultaneously with B3 passing A1 in one frame, in other frames they will set themselves to read zero earlier than or later than the moment B3 passes A1.

?? If the B's can observe B3 passing A1 and the A's can observe A1 passing B3. If they all synchroise their watches to the time this event happens in their own f.o.r, at the instant that they observed the event, don't they all agree on the exact time their watches show when the event happened ??

No, because the Bs are using a different frame's definition of simultaneity than the As, are they not? If I'm understanding you, B1 and B2 set their watches to 0 "simultaneously" with B3 passing A1 as defined in the B rest frame, while A2 and A3 set their watches to 0 "simultaneously" with B3 passing A1 as defined in the A rest frame. Tell me if I got that wrong, but if not, you understand that the A rest frame and the B rest frame define simultaneity differently, right? So it should be no surprise that in the B rest frame, A2 and A3 do not set their watches to 0 at the same moment B3 passes A1, and likewise in the A rest frame, B1 and B2 do not set their watches to 0 at the same moment B3 passes A1.

If the A1 synchs with B3 and then the A's synch their watches with A1 in their f.o.r and the B's synch their watches with B3 in their f.o.r, aren't all of the watches synch'd to each other in both f.o.r's at that moment, but then the times on A's and B's watches drift apart afterwards ?

No, again because what distant clocks read "at that moment" is a question of simultaneity, and the B rest frame defines simultaneity differently from the A rest frame.

So 'locally' means at the same time & place

yup.

and 'simultaneously' means a single event viewed from our super-human viewing point, but potentially viewed as happening at different times from different f.o.r's ?

"Simultaneously" refers to the question of whether two different events happening at different points in space happened "at the same time" or not. And if "our super-human viewing point" is taken to mean a view of spacetime as a whole, there is no "objective" answer from this viewing point as to whether two events happened simultaneously, any more than a person viewing a piece of paper with two dots on it would say there's an objective answer to whether both dots share the same y-coordinate, it all depends on where you place your coordinate axes (assume no coordinate axes are drawn on the paper, the observer has to lay coordinate axes on himself, so it's up to him to decide how they're oriented). The super-human view of spacetime sees that there are different ways you could lay space and time axes on spacetime, corresponding to different reference frames--for two events with a spacelike separation, there would be one orientation that would give the events the same t-coordinate (so they happen 'simultaneously'), while other orientations give them different t-coordinates. A lot of this would probably be more intuitive to you if you learned the basics of using minkowski diagrams in SR (http://en.wikibooks.org/wiki/Special_Relativity:_Simultaneity,_time_dilation_and_length_contraction seems to have a decent tutorial), since they actually show the orientation of the space and time axes for different frames.

Is there a term for a single event witnessed within a single f.o.r by multiple observers at different places, ie. All the B's viewing B3 pass by A1 ? An f.o.r-local event ?

What do you mean by "viewing"? We aren't talking about the time they actually see the light from the event of B3 passing A1, are we? I assumed that B1 and B2 would set their clocks to 0 "at the same time" in their rest frame that B3 passed A1, which would be well before the light from this event would actually reach them and they could see it happening. So talking about them "witnessing" the event doesn't really make sense to me, they've just calculated what time on their watches will be simultaneous with that event in their rest frame, and at that moment they reset their watches to 0.

Again, apologies. All 6 sync their watches to when they observe A1 & B3 pass each other.

Again, by "observe" I'm presuming you don't mean the time they actually see the light from this event, but just that they set their watches to 0 at the time that is simultaneous with this event in their own rest frames (with the As using a different definition of 'simultaneous' than the Bs)?

As the event is local to A1 & B3 it's also a common event for A2, A3, B2 & B3 ?

What do you mean by "also a common event"? It's true that no matter what frame you use, the event of A1 setting his clock to 0 and the event of B3 setting his clock to 0 are simultaneous, since these two events are local. But the event of any other observer like A2, A3, B2 or B3 setting their own clock to 0 is a separate event happening at a different position in space, so different frames disagree on whether, for example, the event of B2 setting his watch to 0 happens simultaneously with the event of A1 passing B3.

The A's will all agree on an event in their f.o.r and the B's will all agree on an event in their f.o.r ?

Yes, but three clocks at different locations setting their time to 0 is not "an event", it is three different events. An event is something that happens at a single point in time and space, like a single watch reading a particular time...a single dot in a minkowski diagram. The A's all agree that A1 and B3 set their time to 0 at the moment they passed, since these two events happen locally, but they don't agree that B1 and B2 set their times to 0 at the same moment, since those two events happened at different times in the A rest frame.

Are the rules :

* Time dilation @ 0.6c = 0.8.
* Length contraction @ 0.6c = 1.25

Yes, assuming you're talking about dilation from the rate the clock is ticking in its own rest frame, and contraction from the object's length in its own rest frame.

* 'Local' events are events happening at the same point in space and are viewed as happening simultaneously by anyone at that point in space, in all f.o.r's.

Basically yes, although you don't have to be "at that point in space" to say the events happened simultaneously--your judgement about simultaneity has nothing to do with where you are located, it only depends on what frame you are using (usually we adopt the convention that 'your' frame means your rest frame, although of course you are actually free to calculate things from the perspective of some other frame).

* Simultaneous events are events that happen at the same time but may be viewed as happening at different times from different f.o.r's ?

No, there is no objective answer to whether two events "happen at the same time". Simultaneity is a completely frame-dependent concept, all you can say is whether two events happen simultaneously (same time-coordinate) or non-simultaneously (different time coordinates) in a particular f.o.r.

* All observers within a single f.o.r will observe an event happening at the same time. (f.o.r-local event ?).

Provided by "observe" you just mean the time-coordinate that will be assigned to that event, and not the time the light from the event actually reaches them, then yes, if they're all using the same f.o.r. then they will all assign the same time-coordinate to a given event. But I wouldn't use the term "f.o.r.-local event" for this, I don't think it really needs a term at all, it's just a tautology that if two people use the same coordinate system, they'll assign the same coordinates to every event.

* All rules must work the same in any f.o.r.

Yes.

 

[M1keh]

As jtbell said, it is understood that the lorentz contraction formula tells you how much a ruler's length will be shrunk from its length in its own rest frame. Now, you could come up with a general formula that tells you "if an object's length in your frame is L and its speed in your frame is v1, what is its length in a frame which is moving at speed v2 in the same/the opposite direction", and this formula would work the same way in every frame, but the lorentz contraction formula is not it.

Is that true ? I'm still relatively new to all this, but the Lorentz transformations are used for conversions from one rest frame to another, nothing more ?

The fact that two objects are moving in A's rest frame doesn't change the way we calculate the distance between them in B's rest frame ? The formulae are dependent on the relationship between the two rest frames, nothing more ?

If A measures two 'stationary' objects as 6ly apart and two 'moving' objects as 6ly apart, both must appear as 4.8ly apart to B (moving at 0.6c). Both distances are contracted by a factor of 1.25 ?

Or have I missed something ?

OK, as I said that isn't the way "local" is used in relativity, but I think I understand what you're saying now. In the B rest frame, B1 and B2 will read 0 at the same time B3 passes A1, and in the A rest frame, A2 and A3 will read 0 at the same time B3 passes A1, is that correct? No, because the Bs are using a different frame's definition of simultaneity than the As, are they not? If I'm understanding you, B1 and B2 set their watches to 0 "simultaneously" with B3 passing A1 as defined in the B rest frame, while A2 and A3 set their watches to 0 "simultaneously" with B3 passing A1 as defined in the A rest frame. Tell me if I got that wrong, but if not, you understand that the A rest frame and the B rest frame define simultaneity differently, right? So it should be no surprise that in the B rest frame, A2 and A3 do not set their watches to 0 at the same moment B3 passes A1, and likewise in the A rest frame, B1 and B2 do not set their watches to 0 at the same moment B3 passes A1. No, again because what distant clocks read "at that moment" is a question of simultaneity, and the B rest frame defines simultaneity differently from the A rest frame.

Hmmm. If A1 & B3 can agree on the exact time and B1 & B2 can agree with B3 on the exact time, surely B1 & B2 are agreeing with A1 ? Albeit only for that single moment ?

The same should follow for A2 & A3, meaning that all 6 agree on the exact time of the event where A1 & B3 meet ?

(Yes. let's stick with 'observed' in the GR sense, not allowing for the time light takes to travel in each rest frame).

yup. ... --your judgement about simultaneity has nothing to do with where you are located, it only depends on what frame you are using

So all of the B's would agree that B3 is at A1 and all of the A's would agree that A1 is at B3 ?

(usually we adopt the convention that 'your' frame means your rest frame, although of course you are actually free to calculate things from the perspective of some other frame). No, there is no objective answer to whether two events "happen at the same time". Simultaneity is a completely frame-dependent concept, all you can say is whether two events happen simultaneously (same time-coordinate) or non-simultaneously (different time coordinates) in a particular f.o.r. Provided by "observe" you just mean the time-coordinate that will be assigned to that event, and not the time the light from the event actually reaches them, then yes, if they're all using the same f.o.r. then they will all assign the same time-coordinate to a given event. But I wouldn't use the term "f.o.r.-local event" for this, I don't think it really needs a term at all, it's just a tautology that if two people use the same coordinate system, they'll assign the same coordinates to every event. Yes.

When you move from A's rest frame, measuring the distance between two objects as 6ly, to B's rest frame, traveling at 0.6c relative to A, B MUST measure the distance as 4.8ly ? 6.0ly * 0.8 ??

Is this correct ?

Is this one of the necessary outcomes of the 'laws of physics' as we now know them ?

 

[jtbell]

Is that true ? I'm still relatively new to all this, but the Lorentz transformations are used for conversions from one rest frame to another, nothing more ?

The Lorentz transformation equations relate the position and time of an event in one inertial reference frame to the position and time of the same event in another inertial reference frame:

$$x^{\prime} = \gamma (x - v t)$$

$$t^{\prime} = \gamma (t - v x / c^2)$$

They always apply, between any two inertial reference frames.

The familiar length contraction equation relates the length of an object (or distance between two objects) in its (their) own rest frame to its (their) length in another inertial reference frame. It is more restricted in application than the Lorentz transformation equations, in that one of the frames must be the object's rest frame.

You might be confusing the length contraction and time dilation formulas with the Lorentz transformation equations. They are different, although related in that one can derive the length contraction and time dilation formulas from the Lorentz transformation equations.

If A measures two 'stationary' objects as 6ly apart and two 'moving' objects as 6ly apart, both must appear as 4.8ly apart to B (moving at 0.6c). Both distances are contracted by a factor of 1.25 ?

No, they are not. The objects that are stationary (and 6 ly apart) in frame A are indeed 4.8 ly apart in frame B. The objects that are moving (and 6 ly apart) in frame A are a different distance apart in frame B; that distance depends on how fast they are moving in frame A, as well as on the relative velocity of frames A and B.

The difference in the two situations can be explained using relativity of simultaneity. In order to measure the distance between two moving objects in any frame, you must measure their positions simultaneously, whereas if the objects are stationary, you don't have to measure their positions simultaneously. I have to go out for the rest of the day soon, but tonight or tomorrow I can probably come up with a worked-out example, unless JesseM beats me to it.

 

[JesseM]

As jtbell said, it is understood that the lorentz contraction formula tells you how much a ruler's length will be shrunk from its length in its own rest frame. Now, you could come up with a general formula that tells you "if an object's length in your frame is L and its speed in your frame is v1, what is its length in a frame which is moving at speed v2 in the same/the opposite direction", and this formula would work the same way in every frame, but the lorentz contraction formula is not it.

Is that true ? I'm still relatively new to all this, but the Lorentz transformations are used for conversions from one rest frame to another, nothing more ?

Sorry about the confusion there, Lorentz contraction is just a synonym for length contraction, it refers to the formula $$L = L_0 \sqrt{1 - v^2/c^2}$$, while the Lorentz transformation is a general set of equations for transforming the coordinates of one frame to the coordinates of another. In the above quote I was talking about the Lorentz contraction formula, not the Lorentz transformation.

The fact that two objects are moving in A's rest frame doesn't change the way we calculate the distance between them in B's rest frame ? The formulae are dependent on the relationship between the two rest frames, nothing more ?

No, the Lorentz contraction formula is based on an object's speed in the frame you're using, and on the object's rest length in its own rest frame. As I said above, though, it would be relatively simple to come up with a new formula that tells you "if an object's speed in my frame is v1 and its length in its direction of motion in my frame is L, what is its length in another frame which is moving at speed v2 in the same/opposite direction as the object's direction of motion", but this would be a different formula from the Lorentz contraction formula $$L = L_0 \sqrt{1 - v^2/c^2}$$.

If A measures two 'stationary' objects as 6ly apart and two 'moving' objects as 6ly apart, both must appear as 4.8ly apart to B (moving at 0.6c). Both distances are contracted by a factor of 1.25 ?

No, again, the contraction factor in the Lorentz contraction formula is contraction from the object's rest length.

Hmmm. If A1 & B3 can agree on the exact time and B1 & B2 can agree with B3 on the exact time, surely B1 & B2 are agreeing with A1 ? Albeit only for that single moment ?

Yes, if A1 and B3 both read 0 at the same moment ('at the same moment' in all frames, since these events are local), then in the B-frame, B1, B2, B3 and A1 all read 0 at the same moment in the B-frame (but aside from B3 and A1, these events do not all happen simultaneously in other frames, since they occur at distinct locations in space).

The same should follow for A2 & A3

Yes, if by "the same" you mean that in the A-frame, B3, A1, A2 and A3 all read 0 at the same moment in the A-frame (but again, aside from B3 and A1, these events do not all happen simultaneously in other frames).

meaning that all 6 agree on the exact time of the event where A1 & B3 meet ?

No--again, you have to keep track of which frame you're talking about. In the B-frame, at the "same moment" that B1, B2, B3 and A1 all read 0, A2 reads 3.6 years and A3 reads 7.2 years. And in the A-frame, at the "same moment" that B3, A1, A2 and A3 all read 0, B2 reads 2.88 years and B1 reads 5.76 years. There is no inertial frame where all 6 read 0 simultaneously.

So all of the B's would agree that B3 is at A1 and all of the A's would agree that A1 is at B3 ?

In both the B-frame and the A-frame, there would be a single moment when B3 and A1 are passing and their clocks both read 0. But if you're trying to compare the times in the two frames, asking whether the A's see A1 meeting B3 "at the same time" that the B's see them meeting, that question wouldn't really make sense (aside from the question of whether both frames assign the same time-coordinate to these events, but that can be changed just by moving the temporal origin of one frame's coordinate system, which is no more significant than moving the spatial origin of your x, y and z axes). The two frames aren't like two movies playing in parallel where we can ask what's happening on the two screens "at the same time" from our perspective in the theater, the phrase "at the same time" is only used for talking about simultaneity within a particular frame.

When you move from A's rest frame, measuring the distance between two objects as 6ly, to B's rest frame, traveling at 0.6c relative to A, B MUST measure the distance as 4.8ly ? 6.0ly * 0.8 ??

Is this correct ?

No, see above on how the Lorentz contraction formula works.

 

[Thrice]

Jesse are you the same IIDB jesse? If so, will you marry me? :p

 

[JesseM]

Jesse are you the same IIDB jesse? If so, will you marry me? :p

Yup, one and the same. But marriages based solely on a shared love of physics rarely work out ;) Are you on IIDB yourself?

 

[Thrice]

I'm on IIDB too, yeah. Come to think of it, I may have gotten the link to this forum from you many months ago. Physics people are few & far between. I'd spend all my time here if these forums were more active.

 

[M1keh]

The Lorentz transformation equations relate the position and time of an event in one inertial reference frame to the position and time of the same event in another inertial reference frame:

$$x^{\prime} = \gamma (x - v t)$$

$$t^{\prime} = \gamma (t - v x / c^2)$$

Ouch. More maths. :-( ... inevitable I guess.

Ah. Okay. So the $$\sqrt{1 - v^2/c^2}$$ is just the start of it and a specialisation of the real formula ?

Ok. Apologies for my ignorance, but the notation used isn't familiar.
$$t^{\prime}$$
$$\gamma (t - v x / c^2)$$ ? Is the $$\gamma$$ just a shorthand for $$\sqrt{1 - v^2/c^2}$$ ?

They always apply, between any two inertial reference frames.

The familiar length contraction equation relates the length of an object (or distance between two objects) in its (their) own rest frame to its (their) length in another inertial reference frame. It is more restricted in application than the Lorentz transformation equations, in that one of the frames must be the object's rest frame.

But not if the distance between moving objects is measured in their own rest frame ? This only applies to stationery objects ?

You might be confusing the length contraction and time dilation formulas with the Lorentz transformation equations. They are different, although related in that one can derive the length contraction and time dilation formulas from the Lorentz transformation equations.

No. But I had made assumptions about the application of the formulae above. Having not understood them properly.

No, they are not. The objects that are stationary (and 6 ly apart) in frame A are indeed 4.8 ly apart in frame B. The objects that are moving (and 6 ly apart) in frame A are a different distance apart in frame B; that distance depends on how fast they are moving in frame A, as well as on the relative velocity of frames A and B.

The difference in the two situations can be explained using relativity of simultaneity. In order to measure the distance between two moving objects in any frame, you must measure their positions simultaneously, whereas if the objects are stationary, you don't have to measure their positions simultaneously. I have to go out for the rest of the day soon, but tonight or tomorrow I can probably come up with a worked-out example, unless JesseM beats me to it.

Oh, bugger. Missed this completely.

I'll need to understand how these formulae work. Are they complicated or relatively straight forward ?

 

[jtbell]

Following up on posting #114... I wrote all of this offline and pasted it into the reply window. I haven't found any problems with the LaTex equations or other typos yet, but don't take that as a guarantee!

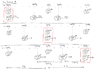
Here's a worked-out example that uses the Lorentz transformation equations to calculate the distance between two objects in frame B, (a) when the objects are at rest in frame A, and (b) when the objects are moving in frame A. It shows that the well-known length contraction formula gives the correct result for (a) but not for (b).

The setup: in frame A we have two objects, 1 and 2. Alternatively, they could be the two ends of a single object. Assume that in frame A at time 0 they have coordinates $x_1 = 0$ and $t_1 = 0$ at one end and $x_2 = 6$ and $t_2 = 0$ at the other end. Imagine little flashbulbs going off on both objects at time 0, if you like.

Frame B is moving to the right at 0.6c with respect to frame A, so $\gamma = 1 / \sqrt {1 - v^2 / c^2} = 1.25$.

The Lorentz transformation equations are

$$x^\prime = \gamma (x - v t)$$

$$t^\prime = \gamma (t - v x / c^2)$$

We'll use units of light-years for distance and years for time, so c = 1 and we can omit c from our equations to simplify them.

Case (a): The objects are stationary in frame A

We use the Lorentz transformation to find the coordinates of the two objects in frame B. First let's try

$$x_1^\prime = \gamma (x_1 - v t_1) = 1.25 (0 - 0.6 \cdot 0) = 0$$

$$t_1^\prime = \gamma (t_1 - v x_1) = 1.25 (0 - 0.6 \cdot 0) = 0$$

$$x_2^\prime = \gamma (x_2 - v t_2) = 1.25 (6 - 0.6 \cdot 0) = 7.5$$

$$t_2^\prime = \gamma (t_2 - v x_2) = 1.25 (0 - 0.6 \cdot 6) = -4.5$$

We expect the distance between the two objects in frame B to equal $x_2^\prime - x_1^\prime = 7.5 - 0 = 7.5$. But this can't be right, because it should be contracted to $L_0 / \gamma = 6 / 1.25 = 4.8$, according to the length contraction equation!

The problem is that $t_1^\prime$ and $t_2^\prime$ are different. In frame B, the two objects are moving, so we have to measure their positions at the same time in order to calculate the distance between them using $x_2^\prime - x_1^\prime$. Because of the relativity of simultaneity, two events at different locations that are simultaneous in frame A are not simultaneous in frame B, and vice versa.

We need to find $x_2^\prime$ when $t_2^\prime = 0$, not when $t_2^\prime = -4.5$. This means we can't use $t_2 = 0$ in the Lorentz transformation, but must leave it unknown instead. Nevertheless, we can still use $x_2 = 6$ because object 2 is stationary in frame A, that is, it's always at that position no matter what time it is. (I've put this in boldface because it's a crucial assumption that we're going to return to later.)

So our two Lorentz transformation equations for object 2 now become (substuting $t_2^\prime = 0$ and leaving $t_2$ unknown)

$$x_2^\prime = 1.25 (6 - 0.6 t_2)$$

$$0 = 1.25 (t_2 - 0.6 \cdot 6)$$

Solving these gives us $x_2^\prime = 4.8$ and $t_2 = 3.6$. Now we can calculate the distance between the two objects in frame B as $x_2^\prime - x_1^\prime = 4.8 - 0 = 4.8$, which agrees with the result from the length contraction equation.

Case (b): The objects are moving in frame A

Now, let's suppose the two objects are both moving to the right in frame A, at speed 0.8c. At time 0 they have the same coordinates that we assumed before. The only difference is that now, they're moving.

For object 1, we can use the Lorentz transformation just like before, to get $x_1^\prime = 0$ and $t_1^\prime = 0$.

For object 2, we can follow similar reasoning as before, up to the assumption that I put in boldface earlier. We cannot now use $x_2 = 6$ because the object is moving. Object 2 is at position $x_2 = 6$ only at time $t_2 = 0$, in frame A. But now $t_2$ is unknown, so $x_2$ is also unknown, and the Lorentz transformation equations for object 2 now look like this:

$$x_2^\prime = 1.25 (x_2 - 0.6 t_2)$$

$$0 = 1.25 (t_2 - 0.6 x_2)$$

We have two equations for three unknowns, which are impossible to solve, as is. We need another equation! Fortunately, object 2 moves at constant velocity 0.8 ly/yr in frame A, starting from $x_2 = 6$ at $t_2 = 0$, so we can easily write down an equation which tells where object 2 is at any time, in frame A (its equation of motion):

$$x_2 = 6 + 0.8 t_2$$

We now have three equations in three unknowns. We can easily solve them to get $t_2 = 6.923$, $x_2 = 11.539$, and $x_2^\prime = 9.231$.

Therefore the distance between the two objects (which are moving in frame A) is $x_2^\prime - x_1^\prime = 9.231 - 0 = 9.231$ ly in frame B, whereas we got 4.8 ly in case (a).

Appendix

There's a way we can verify our answer for case (b) without using the Lorentz transformation equations. I'll describe the steps and show the results here, and leave it as an exercise for the reader to perform the calculations.

Step 1: The distance between the moving objects in frame A is already length-contracted, so use the length-contraction equation "backwards" to find the proper distance between them. That is, find the distance between the objects in the reference frame in which they are at rest. I'll call this frame R. The proper distance turns out to be 10 ly.

Step 2: Use the relativistic "velocity addition" equation to find the velocity of frame B relative to frame R, given that the velocity of frame R relative to frame A is 0.8 ly/yr and the velocity of frame B relative to frame A is 0.6 ly/yr. This velocity turns out to be 0.3846 ly/yr.

Step 3: Use the length contraction equation with the velocity found in step 2, to find the distance between the objects in frame B. This turns out to be 9.231 ly. (Surprise! )

 

[JesseM]

Ouch. More maths. :-( ... inevitable I guess.

Ah. Okay. So the $$\sqrt{1 - v^2/c^2}$$ is just the start of it and a specialisation of the real formula ?

Ok. Apologies for my ignorance, but the notation used isn't familiar.
$$t^{\prime}$$
$$\gamma (t - v x / c^2)$$ ? Is the $$\gamma$$ just a shorthand for $$\sqrt{1 - v^2/c^2}$$ ?

$$\gamma$$ is the inverse of that, $$\frac{1}{\sqrt{1 - v^2/c^2}}$$. Note that I discussed the use of the Lorentz transformation formula, and gave an example, back in the second half of my post #65 earlier on the thread. And as jtbell shows, the length contraction formula can be derived from the Lorentz transformation, as can the other specialized formulas we've discussed like time dilation and the equation that shows how out-of-sync moving clocks will be if they are synchronized in their rest frame.

 

[M1keh]

Wow. Thanks.

Obviously, this will take some time to go through. Should keep me quiet for a while. :-)

 

[M1keh]

$$\gamma$$ is the inverse of that, $$\frac{1}{\sqrt{1 - v^2/c^2}}$$. Note that I discussed the use of the Lorentz transformation formula, and gave an example, back in the second half of my post #65 earlier on the thread. And as jtbell shows, the length contraction formula can be derived from the Lorentz transformation, as can the other specialized formulas we've discussed like time dilation and the equation that shows how out-of-sync moving clocks will be if they are synchronized in their rest frame.

Thanks folks.

I thought there must have been some details I was missing.

These will take a bit of time to digest. A bit of light reading for tonight :-)

 

[M1keh]

You break down the path into units of constant-velocity motion, but you use a single inertial frame to calculate how much time elapses on both the traveling clock and the Earth clock during each unit. No, because again, different inertial frames define simultaneity differently. At the instant of turnaround in the traveling twin's outbound rest frame, the time on Earth might be 2010; but at the instant of turnaround in the traveling twin's inbound rest frame, the time on Earth might be 2020. So, you'd get the wrong answer if you tried to figure out the total time elapsed on Earth between departure and return by saying something like "the ship left Earth in 2005, and in the outbound rest frame only 5 years passed on Earth between the moment of departure and the moment of turnaround, then in the inbound rest frame only 5 more years passed on Earth between the moment of turnaround and the moment of return to earth, therefore Earth's clock will read 2015 at the moment of return." This would miss the discontinuous gap between the Earth's time at the moment of turnaround in the outbound frame and the Earth's time at the moment of turnaround in the inbound frame, due to the two frames defining simultaneity differently--because of this gap, the actual time when the ship returned would be 2020 + 5 = 2025, not 2015 as in the naive calculation. If you stick to a single inertial frame for adding each segment you won't run into this sort of problem. OK, let's say our ship departs Earth and travels at 0.6c for 10 years in the Earth's frame, then turns instantaneously and travels back at 0.6c for another 10 years in the Earth's frame. In the Earth's frame, the time dilation factor is $$\sqrt{1 - 0.6^2}$$ = 0.8, so the traveling twin's clock will only tick (10 years)*(0.8) = 8 years during the outbound leg, and (10 years)*(0.8) = 8 years during the inbound leg, so when they reunite the Earth's clock will show 20 years have elapsed while the ship's clock only shows 16. Note that both the 10 years and the 0.8 time dilation factor were calculated solely from the perspective of the Earth's inertial frame.

Now let's analyze the problem in a different inertial frame--the frame where the traveling twin is at rest during the outbound leg. In this frame, the Earth will be moving away at a constant speed of 0.6c, while the ship will first be at rest for 8 years, during which time the Earth has moved away a distance of (8 years)*(0.6c) = 4.8 light years, and its clock has advanced by (8 years)*(0.8) = 6.4 years, while the ship's clock has advanced forward by 8 years since it is at rest. Then after 8 years the ship will accelerate instantaneously, and using the velocity addition formula we know its speed in this frame after acceleration will be (0.6c + 0.6c)/(1 + 0.6^2) = 1.2c/1.36 = 0.88235c. Since the Earth is 4.8 light years away but only moving at 0.6c, the time for the ship to catch up can be found by solving for t in 4.8 + 0.6t = 0.88235t, which gives t = 17 years in this frame. During this time, the Earth's time dilation factor will still be 0.8, while the ship's will be $$\sqrt{1 - 0.88235^2}$$ = 0.4706, so the Earth's clock will have advanced forward by (17 years)*(0.8) = 13.6 years while the ship's clock will have advanced forward by (17 years)*(0.4706) = 8 years. So, by the time the ship catches up to the earth, the Earth's clock will have advanced forward by the 6.4 years of the outbound leg plus the 13.6 years of the inbound leg, while the ship's clock will have advanced by the 8 years of the outbound leg plus the 8 years of the inbound leg. So, we find that the Earth's clock had advanced 20 years while the ship's clock has advanced only 16, just as we found in the Earth's frame.

We could also analyze everything from the point of view of the frame where the ship is at rest during the inbound leg. This will just be the mirror image of how things looked in the outbound rest frame--during the outbound leg, the Earth is moving at 0.6c while the ship is moving at 0.88235c in the same direction, which lasts for 17 years, then the ship instantaneously accelerates and comes to rest while the Earth continues to approach it at 0.6c from a distance of 4.8 light years, catching up to it after 8 years in this frame. And again, in a mirror image of the analysis in the outbound rest frame, the ship's clock elapses (17)*(0.4706) = 8 years during the outbound leg and (8)*(1) = 8 years in the inbound leg, while the Earth's clock elapses (17)*(0.8) = 13.6 years in the outbound leg and (8)*(0.8) = 6.4 years in the inbound leg, so you again predict the ship's clock elapses a total of 16 years while the Earth's clock elapses a total of 20 years.

Now look what would happen if you tried to switch frames in mid-problem, without worrying about simultaneity issues. Start out using the outbound rest frame during the outbound leg, and you'll conclude that at the moment before the ship does its instantaneous acceleration, the ship's clock reads 8 years and the Earth is 4.8 light years away, its clock reading 6.4 years. Now if you switch to the inbound rest frame, and you don't realize that because of the different definition of simultaneity the Earth should "jump" to reading 13.6 years, then you'll mistakenly continue to think that at the beginning of the inbound leg the Earth's clock reads 6.4 years, and since the inbound frame says the ship is at rest during the inbound leg while the Earth is approaching it at 0.6c from 4.8 light years away, in the inbound frame the ship's clock must advance by 8 years during the inbound leg and the Earth's clock must advance by (8)*(0.8) = 6.4 years, so you would conclude the Earth's clock only read 6.4 + 6.4 = 12.8 years when the ship returned? But this answer contradicts the answer you get when you stick to a single inertial frame throughout the problem, whether the Earth rest frame, the inbound rest frame or the outound rest frame; you get the wrong answer if you try to "patch together" different frames in mid-problem this way, without taking into account discontinuous jumps in clock time due to the frames defining simultaneity differently. Although the time dilation factor as measured in a given inertial frame is only a function of a clock's speed in that frame, not its velocity, a frame can only qualify as "inertial" in the first place if it is moving at constant velocity, not just constant speed. So even though the instantaneous acceleration means the traveling twin never changed speeds in the Earth's inertial frame (although he did change speeds in every other inertial frame, like the outbound rest frame), he did not stay at rest in a single inertial frame throughout the journey.

Analyzing the triplets problem wouldn't differ much from the twins problem. Let's again assume that in the Earth's frame, the two traveling triplets move at 0.6c, and turn around after 10 years. In the Earth's frame, each traveling triplet ages (10 years)*(0.8) = 8 years during their outbound legs, and another 8 years during their inbound legs, so that they have both aged 16 years when they return while the Earth twin has aged 20 years.

Now look at things from the perspective of an inertial frame where one of the triplets is at rest during the oubound leg. In this frame, for the first 8 years this triplet (call him A) will be at rest, while the earth-triplet (call him B) is moving away at 0.6c and the third triplet (call him C) is moving away at (0.6c + 0.6c)/(1 + 0.6^2) = 0.88235c. Since C's clock is ticking slow by a factor of 0.4706 in this frame, and he won't accelerate until 8 years have passed on his own clock, he won't turn around until 8/0.4706 = 17 years have passed in this frame; when he does turn around, he'll be at rest in this frame, and at this moment the distance between him and the Earth is (17 years)*(0.88235c - 0.6c) = 4.8 light years. The Earth will continue to approach him at 0.6c after this point, reaching him after an additional 4.8/0.6 = 8 years in this frame. And when A turns around after 8 years, he is now moving in the direction of the Earth at 0.88235c, with the Earth having moved a distance of (8 years)*(0.6c) = 4.8 light years in those 8 years. The time for A to catch up to the Earth is given by 4.8 + 0.6t = 0.88235t, or 17 years. So in this frame A starts out at rest, accelerates after 8 years, then takes another 17 years to catch up to earth, while C starts out at high speed, accelerates to rest after 17 years, and then the Earth takes an another 8 years to catch up to him, meaning all three twins reunite after 25 years have passed in this frame.

So now let's figure out how much time has passed on each twin's clock after 8 years, after 17 years, and after 25 years in this frame, using this frame's values of the speeds and time dilation factors.

Between departure and 8 years:
-twin A has been at rest, so 8 years have passed on his clock
-twin B has been moving at 0.6c, giving a time dilation factor of 0.8, so (8 years)*(0.8) = 6.4 years have passed on his clock.
-twin C has been moving at 0.88235c, giving a time dilation factor of 0.4706, so (8 years)*(0.4706) = 3.765 years have passed on his clock.

Between 8 years and 17 years:
-twin A has been moving at 0.88235c, so in the 17-8=9 years of this section, (9 years)*(0.4706) = 4.235 additional years have passed on his clock.
-twin B has been moving at 0.6c, so (9 years)*(0.8) = 7.2 additional years have passed on his clock.
-twin C has been moving at 0.88235c, so 4.235 additional years have passed on his clock.

Between 17 years and 25 years:
-twin A has been moving at 0.88235c, so in the 25-17=8 years of this section, (8 years)*(0.4706) = 3.765 additional years have passed on his clock.
-twin B has been moving at 0.6c, so (8 years)*(0.8) = 6.4 additional years have passed on his clock.
-twin C has been at rest, so 8 additional years have passed on his clock.

If you add all these up, you again find that 20 years passed on twin B's clock while 16 years passed on both A and C's clocks between the beginning and end of the journey; also, twin A and C's clocks each registered 8 years before they turned around and 8 years after. This got a bit complicated, so let me know if there's any steps you don't follow.

Just noticed something.

If, from A's f.o.r, in the first 8 years A is stationery and B is 0.6c, then the furthest distance between A and B, according to A is 4.8 ly ? According to B this is 8 ly ? So did A reach his destination 8 ly from B or not ?

He would have had to measure his distance from B as 6.4 ly to have reached the destination ?

 

[JesseM]

Just noticed something.

If, from A's f.o.r, in the first 8 years A is stationery and B is 0.6c, then the furthest distance between A and B, according to A is 4.8 ly ? According to B this is 8 ly ? So did A reach his destination 8 ly from B or not ?

He would have had to measure his distance from B as 6.4 ly to have reached the destination ?

Remember that in the frame of B (the Earth-twin) the traveling twin A was moving away for 10 years instead of 8. So, with their relative speed being 0.6c, the B sees A move 6 light years away before reaching the destination, not 8 light years. In A's frame, this distance is Lorentz-contracted to 6*0.8 = 4.8 light years, so it's consistent.

 

[M1keh]

Doh. Fools rush in ! Thanks.

 

[M1keh]

Remember that in the frame of B (the Earth-twin) the traveling twin A was moving away for 10 years instead of 8. So, with their relative speed being 0.6c, the B sees A move 6 light years away before reaching the destination, not 8 light years. In A's frame, this distance is Lorentz-contracted to 6*0.8 = 4.8 light years, so it's consistent.

Ok. I'm not giving up ...

Instead of journeys out from Earth, how about the same measurements but two travellers traveling towards Earth at 0.6c from two satellites 6ly away from Earth ?

How do the figures work then ??

Now all three start in Earth time so they can synchronise watches ? The travellers instantly accelerate to 0.6c and measure the distances, in their new f.o.r.'s

A will see B as 4.8 ly away and C as 9.6 ly away ?
C will see B as 4.8 ly away and A as 9.6 ly away ?
B will see A as 6 ly away and C as 6 ly away ?

All three view themselves as remaining stationery in their new f.o.r ?

From A's f.o.r :

First 8 years.
* A will remain stationery for 8 years.
* B will travel at 0.6 and his watch will show 0.8 * 8years = 6.4 years and he will have traveled 0.6*8 = 4.8ly.
* C will travel at (0.6+0.6)/(1+0.6^2) = 0.88235c and will travel 0.88235*8 = 7.06 ly. Watch will have moved 3.765 years.

Now, B's watch must be 1.6 years earlier than A's, C's watch must be 4.235 years before A's and C won't have reached A ?


What's wrong ?

 

[JesseM]

Ok. I'm not giving up ...

Instead of journeys out from Earth, how about the same measurements but two travellers traveling towards Earth at 0.6c from two satellites 6ly away from Earth ?

How do the figures work then ??

Now all three start in Earth time so they can synchronise watches ? The travellers instantly accelerate to 0.6c and measure the distances, in their new f.o.r.'s

A will see B as 4.8 ly away and C as 9.6 ly away ?
C will see B as 4.8 ly away and A as 9.6 ly away ?
B will see A as 6 ly away and C as 6 ly away ?

That's right.

edit: sorry, that's actually not quite right. In the frame of reference where A is at rest after acceleration, it's true that C was 9.6 light years from A before either C or A accelerated. However, in this frame C accelerated well before A (see below), so at the moment A accelerates C has already been traveling towards B for some time, so the distance is smaller. Something analogous is true in the frame where C is at rest after accelerating.

All three view themselves as remaining stationery in their new f.o.r ?

From A's f.o.r :

First 8 years.
* A will remain stationery for 8 years.
* B will travel at 0.6 and his watch will show 0.8 * 8years = 6.4 years and he will have traveled 0.6*8 = 4.8ly.

Yes.

* C will travel at (0.6+0.6)/(1+0.6^2) = 0.88235c

Right.

and will travel 0.88235*8 = 7.06 ly. Watch will have moved 3.765 years.

This part is wrong, you're forgetting that in this frame, although C was 4.8 ly from B at the moment before it accelerated, after it accelerates B is still moving away from it at 0.6c, so C is only gaining on B at a speed of 0.88235c - 0.6c = 0.28235c. Also, because of the relativity of simultaneity, C accelerated much earlier than A in this frame.

The main thing you're forgetting is that even though all their clocks were synchronized at the moment of acceleration in the Earth's inertial rest frame, in the inertial rest frame where A is at rest after the acceleration, the three clocks were not synchronized at the moment A accelerated, because of the relativity of simultaneity. If you don't want to use the full Lorentz transform, you can use the formula vx/c^2 to figure out how out-of-sync the clocks are before any of them accelerate, in the frame where A is at rest after acceleration: here, x is the distance between two synchronized clocks in their own rest frame, and v is their velocity in your frame. Since A and B are 6 ly apart in their mutal rest frame before acceleration, in a frame moving at 0.6c relative to them, B will be ahead of A by (0.6c)(6 ly)/c^2 = 3.6 years. Likewise, C will be ahead of B by a constant factor of 3.6 years until it accelerates, in this frame. So since C accelerates when its own clock reads 0, in this frame A's clock read -7.2 years at the moment C accelerated. And since A's clock is ticking at 0.8 the normal rate until it accelerates, it takes 7.2/0.8 = 9 years in this frame before A's clock reads 0, at which point B's clock reads 3.6 years. Since C has been moving at 0.88235 c during these nine years, C's clock has been moving at 0.4706 the normal rate, so it only moved by 9*0.4706 = 4.235 years. It read 0 at the beginning of the 9 years, so it now reads 4.235 years.

So, in this frame, when A accelerates and comes to rest, A reads 0, B reads 3.6 years, and C reads 4.235 years. It takes 8 years for B to reach A in this frame, so during that time A ticks at the normal rate and advances to 0 + 8 = 8 years, B ticks at 0.8 times the normal rate and advances to 3.6 + 0.8*8 = 10 years, and C ticks at 0.4706 times the normal rate and advances to 4.235 + 0.4706*8 = 8 years. This is the point where they all meet, and the predictions about each one's clock-reading when they meet is the same as what you'd predict in the Earth's rest frame.

 

[M1keh]

Need to think about this some more ...

Yes. That does follow :

Following the same rules, if A, B and C all accelerate to 0.6c in the same direction, they will no longer be showing a synchronised time ? If A is 0y, B will be +3.6y and C will be +7.2y ?

Is this correct ?

 

[JesseM]

Following the same rules, if A, B and C all accelerate to 0.6c in the same direction

I assume you mean they were originally synchronized in their mutual rest frame before accelerating, and they all accelerate "at the same time"? But "at the same time" according to which frame's definition of simultaneity? Do they all accelerate at the same time in the frame where they were initially at rest, or in the frame where they come to rest after accelerating?

they will no longer be showing a synchronised time ? If A is 0y, B will be +3.6y and C will be +7.2y ?

If they all accelerate at the same time in the frame where they are at rest after accelerating, then since they were each out-of-sync with their neighbor by 3.6 years before accelerating (when they were all moving at 0.6c in this frame), and since their clocks will all speed up simultaneously when they come to rest in this frame, they will remain out-of-sync by the same amount. If they were all moving in the direction of A in this frame, so A was at the front and C was at the back, then your figures would be right. On the other hand, if they were all moving in the direction of C, then if A was 0y, B would be -3.6y and C would be -7.2 years--the clock in the back is the one whose time is ahead of the clock in the front.