Can this 4 bit adder be further simplified?

[Psinter]

Hello, I'm new to logic circuits and I was making a 4 bit binary adder and I thought I could maybe simplify it. However, I can't find anything simpler than what I already got. What I wanted to know is: is my circuit already in its most simple form or am I making something wrong in my attempts to simplificate it (meaning it can still be simplificated)?

The circuit works as follows:

We have the 1st 4 bit number: ABCD
We have the 2nd 4 bit number: EFGH

The total sum with one bit at a time would be: (D + H) and (C + G) and (B + F) and (A + E). In other words:
ABCD
EFGH
---------
XXXX

where, (D + H) is the only one that doesn't receive any carry because it's the initial point.

So I need 4 outputs with their respective carries as illustrated:

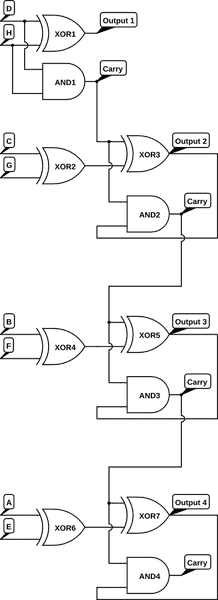
As you can see the pattern of circuits start at the second sum. Meaning, (C + G), (B + F), and (A + E) are the same circuits. I tried to simplify 1 of them so I could simplify the rest of the adder. However, I can't find any way to simplify it any further. When I look at the Karnaugh Map I made out of the Truth Table of the circuit that repeats I don't know what to do from there because I don't have any mapping groups there.


Truth Table: ((C \oplus G) \oplus CARRY) \wedge CARRY
\begin{array}{|c|c|c|c|}
\hline
C & G & CARRY & F1 \\ \hline
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 1 & 1 \\ \hline
0 & 1 & 0 & 0 \\ \hline
0 & 1 & 1 & 0 \\ \hline
1 & 0 & 0 & 0 \\ \hline
1 & 0 & 1 & 0 \\ \hline
1 & 1 & 0 & 0 \\ \hline
1 & 1 & 1 & 1 \\
\hline
\end{array}


Karnaugh Map: ((C \oplus G) \oplus CARRY) \wedge CARRY
\begin{array}{|c|c|c|c|c|c|}
\hline
& G \wedge CARRY & 00 & 01 & 11 & 10 \\ \hline
C & & & & & \\ \hline
0 & & & 1 & & \\ \hline
1 & & & & 1 & \\
\hline
\end{array}

Does all this mean that I cannot simplify my adder any further?

 

[Psinter]

This is wrong, never mind, this adder is wrongly designed. This is not an adder. It says that 0 + 0 = 1 with carry 1 if the previous sum has a carry of 1. We know that this is not true so this is wrong.

 

[Enthalpy]

I confirm it's wrong, because each pair of bits must enter an AND gate. The XOR doesn't suffice.

If you like circuitry, you can give a look at carry propagation and anticipation, both for adders and counters.

 

[skeptic2]

How do you want to simplify it - by reducing the number of ICs? One way to simplify it would be to replace all the ICs with a PROM. Use the address lines as inputs and the data lines as outputs. For every combination of inputs (all addresses) program the correct output. You could even have one of the output lines designated as a carry out and one of the inputs as carry in. That way they could be cascaded.

 

[Enthalpy]

http://www.physics.wisc.edu/undergrads/courses/fall2012/623/ds/74LS283.pdf
http://en.wikipedia.org/wiki/Adder_(electronics)
http://www.google.de/search?q="4+bi...DsbZsgbDpYHoCQ&ved=0CB4QsAQ&biw=1200&bih=1728

Beware that what was a "simple" design with TTL gates isn't "simple" with present-day CMOS, and a "simple" breadboard isn't a "simple" chip design - a simple breadbord would buy a 4-bit full adder chip...

Especially, CMOS can make good XOR gates with 3 inputs, as well as good majority logic gates (= at least 2 inputs of 3 are logical 1).
http://book.huihoo.com/design-of-vlsi-systems/ch06/ch06.html

Interesting : the LS283 computed the carry over 4 bits directly to save time, despite it takes more gates. Again, many-inputs-Nand fit LS very well, and heavy output loading was a small penalty ; different story with CMOS.

Carry lookahead saves time by splitting the 1-bit adder carry signal into a "generate carry" and "propagate carry" (if one carry is input to this bit). These two signals can enter the lookahead unit which, for with words, is a tree.
Depicted here as a binary tree:
http://net.pku.edu.cn/~course/cs101/2007/resource/Intro2Algorithm/book6/chap29.htm
but normally it would be a radix-four tree:
http://pages.cs.wisc.edu/~jsong/CS352/Readings/CLAs.pdf

Carry lookahead exist for counters as well but are easier because a counter passes through FC and FE before attaining FF, giving more time.