Can you just give me a hint for how to solve this problem?

[HAF]

Mentor note = moved to homework hence no template

Good evening everyone. I have a problem with solving this problem. I just don't know where to start. Can you please just "bounce" me somehow?

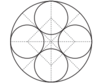
The radius of the big circle is 1m. What is the radius of the small ones?

The only thing I found out is that the diagonal of the small square is 1m. Nothing else.

Can you help me please?

Thank You

 

[tnich]

Good evening everyone. I have a problem with solving this problem. I just don't know where to start. Can you please just "bounce" me somehow?

The radius of the big circle is 1m. What is the radius of the small ones?

The only thing I found out is that the diagonal of the small square is 1m. Nothing else.

Can you help me please?

Thank You
View attachment 227081

I don't think it is correct to say that the diagonal of any in this diagram square is 1. I suggest that you label the picture with what you know already. For example, choose one quadrant containing a small circle and label all of the radii of the small circle as having length $r$. Label the radius of the large circle in that quadrant as having length 1. Now look at the small square formed by the quadrant boundaries and the large square. What is the length of its diagonal?

 

[HAF]

I don't think it is correct to say that the diagonal of any in this diagram square is 1. I suggest that you label the picture with what you know already. For example, choose one quadrant containing a small circle and label all of the radii of the small circle as having length $r$. Label the radius of the large circle in that quadrant as having length 1. Now look at the small square formed by the quadrant boundaries and the large square. What is the length of its diagonal?

So the diagonal of the square in the middle is not 1m? If you are correct than I'm completely lost. Help me please. Can you give me some hints for solving this problem?

 

[tnich]

So the diagonal of the square in the middle is not 1m? If you are correct than I'm completely lost. Help me please. Can you give me some hints for solving this problem?

I gave you some hints in my last post.

 

[HAF]

I gave you some hints in my last post.

Is this thought correct?

 

[jtbell]

You've marked the angle at the top with an arc and a dot. I've never seen that notation. What does it mean?

 

[HAF]

You've marked the angle at the top with an arc and a dot. I've never seen that notation. What does it mean?

I'm sorry for that. This is how I mark right angles.

 

[jtbell]

OK, you have a right triangle. One of the sides adjacent to the right angle has length r. What's the length of the other side (adjacent to the right angle)?

 

[HAF]

OK, you have a right triangle. One of the sides adjacent to the right angle has length r. What's the length of the other side (adjacent to the right angle)?

It's also r i think.

 

[jtbell]

So the hypotenuse of that triangle is...

 

[HAF]

So the hypotenuse of that triangle is...

2r^2

 

[jtbell]

I think that's the square of the hypotenuse.

Anyway, when you've got that sorted out, it gives you part of the radius of the large circle. What's the other part? The two parts have to add to 1.

 

[HAF]

I think that's the square of the hypotenuse.

Yeah I'm sorry. 2^1/2r

 

[jtbell]

2^1/2r

Or (√2)r. Click on the big "sigma" sign at the left, above the message box, and you'll get a palette of symbols that you can enter directly. I used parentheses to make clear that the square root applies only to the 2, not to the r.

Now you can "piece together" the radius of the large circle, which equals 1.

 

[HAF]

Or (√2)r. Click on the big "sigma" sign at the left, above the message box, and you'll get a palette of symbols that you can enter directly. I used parentheses to make clear that the square root applies only to the 2, not to the r.

Now you can "piece together" the radius of the large circle, which equals 1.

Thank You very very much. I don't know why I didn't find it out by myself. I have to practise more.

Thank You guys. You are amazing.

 

[Charles Link]

Did this one get solved yet? I don't see a final answer from the OP @HAF . $\\$ The way I would do it basically uses 2 equations and 2 unknowns: $r$ and a distance $s$ from the origin to where the line $x=0$ intersects the top circle of radius $r$. It's fairly straightforward to write two equations with $r$ and $s$. The one equation is very simple, and the second uses the properties of the 45 degree right triangle. $\\$ If you just consider one circle of radius $r$, the problem can be solved with x and y axes and a circle of radius $r$ that fits into one quadrant. The distance $s$ is then along the line $y=x$, from the origin to where the line first intersects the circle.

 

[HAF]

Did this one get solved yet? I don't see a final answer from the OP @HAF . $\\$ The way I would do it basically uses 2 equations and 2 unknowns: $r$ and a distance $s$ from the origin to where the line $x=0$ intersects the top circle of radius $r$. It's fairly straightforward to write two equations with $r$ and $s$. The one equation is very simple, and the second uses the properties of the 45 degree right triangle. $\\$ If you just consider one circle of radius $r$, the problem can be solved with x and y axes and a circle of radius $r$ that fits into one quadrant. The distance $s$ is then along the line $y=x$, from the origin to where the line first intersects the circle.

Did this one get solved yet? I don't see a final answer from the OP @HAF . $\\$ The way I would do it basically uses 2 equations and 2 unknowns: $r$ and a distance $s$ from the origin to where the line $x=0$ intersects the top circle of radius $r$. It's fairly straightforward to write two equations with $r$ and $s$. The one equation is very simple, and the second uses the properties of the 45 degree right triangle. $\\$ If you just consider one circle of radius $r$, the problem can be solved with x and y axes and a circle of radius $r$ that fits into one quadrant. The distance $s$ is then along the line $y=x$, from the origin to where the line first intersects the circle.

Yeah I solved it. I will definitely use your method also.

I solved it with the right angled triangle.

It's hypotenuse is (√2)r.

(√2)r + r = 1
r= 0,41m

Thank you for your tip Charles.

 

[Charles Link]

Yeah I solved it. I will definitely use your method also.

I solved it with the right angled triangle.

It's hypotenuse is (√2)r.

(√2)r + r = 1
r= 0,41m

Thank you for your tip Charles.

What you did is very similar to how I solved it. The hypotenuse that you computed to be $\sqrt{2} r$ is what I called $r+s$. I saw that $(r+s) \frac{\sqrt{2}}{2}=r$ because of the 45 degree right triangle. And then $(r+s)+r=1$. Your solution is essentially the same thing, and perhaps a step quicker to the answer.

 

[HAF]

What you did is very similar to how I solved it. The hypotenuse that you computed to be $\sqrt{2} r$ is what I called $r+s$. I saw that $(r+s) \frac{\sqrt{2}}{2}=r$ because of the 45 degree right triangle. And then $(r+s)+r=1$. Your solution is essentially the same thing, and perhaps a step quicker to the answer.

Most important thing is that we solved it. :)

Thank You