Area remaining of a quarter-circle deprived of these 3 inscribed circles

[Saracen Rue]

Summary:: Calculate the percentage of area remaining when a quarter-cirlce is deprived of 1 large circles and 2 smaller circles.

Hi,

I'm not sure if this is the right subforum for this question but it seemed to be the one that fit the best. Please consider the following diagram:

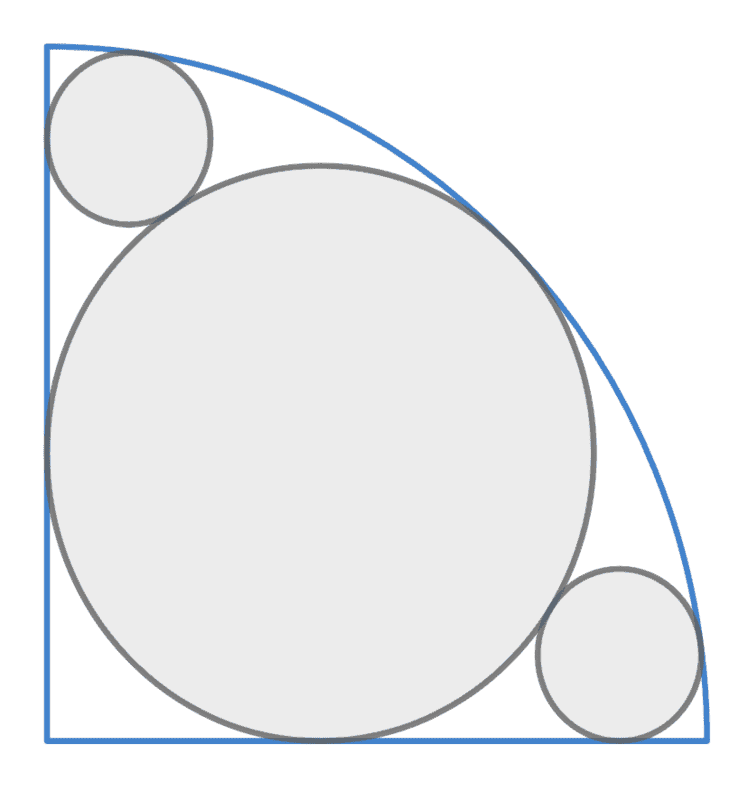
Before continuing, let's quickly define a few things:
$$r_{q} = \text{ radius of the quarter-circle}$$
$$r_{b} = \text{ radius of the big circle}$$
$$r_{s} = \text{ radii of the two smaller circles}$$

I figured out how to express $r_{q}$ in terms of $r_{b}$ with relative ease. With the help of a little Pythagoras I managed to come to the conclusion that
$$r_{q} = (\sqrt{2} + 1) \cdot r_{b}$$

This is a good start, however here's where I hit a brick wall. I have no idea how to go about expressing $r_{s}$ in terms of $r_{b}$. I've tried everything I can think of but I just can't seem to make any progress at all. Any help with solving this problem is greatly appreciated.

Thank you all for your time.

[Moderator's note: Moved from a technical forum and thus no template.]

 

[anuttarasammyak]

Let us think in xy coordinate whose Origin is the rectangular angle.
The center of the right small circle is
$$(x_s,\ y_s)=(r_b+(r_b+r_s)cos\theta,\ r_s)$$
where
$$\sin\theta = \frac{r_b-r_s}{r_b+r_s}$$

This small circle and the quarter circle touch. On the point the both the equations
$$x^2+y^2=r_q^2$$ and
$$(x-x_s)^2+(y-y_s)^2=r_s^2$$
are satisfied. we delete y ( or x )and get a quadratic equation of x ( or y ) which should have one degenerate solution of the touch. The zero discriminant gives us $r_s$.

I have not done detailed calculation by myself. I will appreciate it if you solve it and show us the result.

 

[Saracen Rue]

Let us think in xy coordinate whose Origin is the rectangular angle.
The center of the right small circle is
$$(x_s,\ y_s)=(r_b+(r_b+r_s)cos\theta,\ r_s)$$
where
$$\sin\theta = \frac{r_b-r_s}{r_b+r_s}$$

This small circle and the quarter circle touch. On the point the both the equations
$$x^2+y^2=r_q^2$$ and
$$(x-x_s)^2+(y-y_s)^2=r_s^2$$
are satisfied. we delete y ( or x )and get a quadratic equation of x ( or y ) which should have one degenerate solution of the touch. The zero discriminant gives us $r_s$.

I have not done detailed calculation by myself. I will appreciate it if you solve it and show us the result.

Hi, thank you for the reply. However, I'm still really struggling to make much progress with this problem (my fault entirely).

Solving for the zero discriminant gives us $r_s = y_s$. While this initially seemed quite useful I've really struggled with making any more progress towards expressing $r_s$ in terms of $r_b$. Any more help with this problem is greatly appreciated

 

[anuttarasammyak]

$$(x_s,y_s)=(r_b+2\sqrt{r_b r_s},r_s)$$
$$\frac{r_b}{r_q}=\sqrt{2}-1$$
The quadratic equation of x of contact point of the quarter circle and the right small circle is
$$Ax^2+Bx+C=0$$
where
$$A=4(x_s^2+y_s^2)$$
$$B=-4x_s(x_s^2+y_s^2-r_s^2)$$
$$C=(x_s^2+y_s^2-r_s^2)^2-4y_s^2r_q^2$$
Discriminant is
$$D=B^2-4AC=0$$
$$\frac{1}{4}(\frac{x_s}{r_q})^4-(\frac{x_s}{r_q})^2-(\frac{r_s}{r_q})^2=0$$
Let
$$\sqrt{\frac{r_s}{r_q}}=z$$
the equation D=0 is quartic equation of z.

I am careless in calculation. Please do not trust but check it by yourself.

 

[anuttarasammyak]

EDIT to post #4 : the equation of D=0 was wrong. I would like to replace it by $x_s^4$ equation,

$$(\frac{x_s}{r_q})^4-2(\frac{x_s}{r_q})^2+1-\frac{(\frac{x_s}{r_q}-\frac{r_b}{r_q})^4}{4(\frac{r_b}{r_q})^2} =0$$
The approximate solution is
$$\frac{x_s}{r_q} = 0.867...$$
,so
$$\frac{r_s}{r_q} = 0.176...$$

I should appreciate you would check and verify/correct it.

 

[haruspex]

I get that $\frac{r_s}{r_q}=\frac 1{1+5\sqrt 2}$, which looks about right.
It looked like a quartic at one point, but kept simplifying nicely.

 

[anuttarasammyak]

Thanks harupsex
I checked values in my post#5 and found $\frac{r_s}{r_q}$ should be be revised to 0.12... which meets your answer.

 

[ehild]

With a bit less pain, the centre of the bottom small circle can be obtained as the intersection of a circle concentric with the big one , with radius rq-rs, and an other one, concentric with the inner circle, with radius rb+rs (rs is the radius of the small circle, and the y coordinate of the centre is rs. )
The following system of equations holds:
$r_q=r_b(1+\sqrt2)$
$xs^2+r_s^2=(r_q-r_s)^2$
$(x_s-r_b)^2+(r_s-r_b)^2=(r_b+r_s)^2$
.
I also got xs=0.867 rq and rs=0.124rq

 

[haruspex]

xs=0.867 rq and rs=0.124rq

But exactly $\frac{5\sqrt 2-1}7$ and $\frac 1{5\sqrt 2+1}$ respectively, putting them in the ratio 7:1.

 

[anuttarasammyak]

EDIT to post #5
Ref comment of post #4 the equation is factorized to have three exact real solutions of
$$\frac{x_s}{r_q}=1-\sqrt{2},1+\sqrt{2},\frac{5\sqrt{2}-1}{7}$$

The first one is the case the "small" circle has the same size with the large circle centered at $(-r_b,r_b)$ with one inside another outside letting the quarter circle be the full circle.

The second one is degenerated. It is the case the "small" circle is the biggest one to touch other two circles outsides at $(r_q/\sqrt{2},r_q/\sqrt{2})$.

I should have noticed above for easy factorization. The last one is a reasonable one for us.

 

[ehild]

But exactly $\frac{5\sqrt 2-1}7$ and $\frac 1{5\sqrt 2+1}$ respectively, .

Exactly!

 

[Delta2]

With a bit less pain, the centre of the bottom small circle can be obtained as the intersection of a circle concentric with the big one , with radius rq-rs, and an other one, concentric with the inner circle, with radius rb+rs (rs is the radius of the small circle, and the y coordinate of the centre is rs. )

I just knew that there would be an approach that is a balance of geometrical and analytical approach. What you saying here indicates such an approach, but can you expand abit more on the geometrical side of it, why the intersection of the two aforementioned circles , gives the center of the small circle?

 

[haruspex]

I just knew that there would be an approach that is a balance of geometrical and analytical approach. What you saying here indicates such an approach, but can you expand abit more on the geometrical side of it, why the intersection of the two aforementioned circles , gives the center of the small circle?

Put a straight line through each pair of circle centres (large, small, quadrant) in turn, extending to the contact point as necessary. Since the circles touch, the distances between the centres must be sums and differences of radii.

 

[Delta2]

Put a straight line through each pair of circle centres (large, small, quadrant) in turn, extending to the contact point as necessary. Since the circles touch, the distances must be sums and differences of radii.

Thanks but i feel i have to make a figure myself to see this, i ll try to make a scheme and post it here if it is good enough (i am really bad on making schemes).

 

[ehild]

I just knew that there would be an approach that is a balance of geometrical and analytical approach. What you saying here indicates such an approach, but can you expand abit more on the geometrical side of it, why the intersection of the two aforementioned circles , gives the center of the small circle?

There is a big circle of radius R on both pictures (black) . On the left a small circle of radius r touches the big one from outside. At the common point, the circles have a common tangent, and both radii are normal to it, they make a straight line segment. The centre of the small circle is at distance R+r from the centre of the big one, so it is on the red circle with radius R+r and concentric with the big circle.
On the right picture, the small circle touches the big one from inside. Its centre is at distance R-r from the centre of the big circle, on the red circle of radius R-r és concentric wit the big one.
In the problem, there are two circles, and we want to draw a circle that touches the quarter circle from inside and the inner circle from outside.

 

[benorin]

This is a nice problem. Thanks

 

[anuttarasammyak]

Additive comments to my post #10

Say put a circle in the closed space so that it touches the small circle, x-axis and the quartered circle. We get similar x^4 equation for x coordinate of the center. Now we know the two but degenerated to one solutions for a right outside put circle and one solution for a left circle put outside of the small circle and inside of the quartered circle. After getting these three solution by geometry we can factorize the x^4 equation easily and get the fourth solution we need.

Similar process goes on for putting smaller circles in the spaces.

 

[Saracen Rue]

Hi everyone! I want to apologise for bumping this old thread, but I was recently going through my old posts and found this again. After spending a couple of days having another go at it, I managed to find a solution on my own :) I've decided to share how I went about it here in case anyone else is curious. I suspect it's a rather inefficient way of approaching the problem, but it's just the way I found that got me the correct answer first.

So, before we get started: when I started redoing this problem I made some changes to how I defined the radii for convince sake. So going forward I'll be using the following:
$$q = r_{q} = \text{ radius of the quarter-circle}, \text{ Point } Q = \text{Centre of quarter-circle with radius }q$$
$$b = r_{b} = \text{ radius of the big circle}, \text{ Point } B = \text{Centre of circle with radius }b$$
$$s = r_{s} = \text{ radii of the two smaller circles}$$ $$\text{ Point } S = \text{Centre of the small circle, with radius s, touching the horizonal}$$
As I mentioned in the original post, getting $q$ in terms of $b$ is pretty straight forward. By drawing a line between $Q$ and $B$, we can create a right angled triangle with side lengths $b$ and hypotenuse $\overline{QB}$. From Pythagoras, we can calculate the hypotenuse to be $\sqrt2 b$. From inspection, we can then see that $q=( \sqrt2 b + 1 )b$.

Now, onto the new stuff. The first step I took this time around was to construct another right angled triangle with hypotenuse $\overline{SB}$, like so:

This triangle has a hypotenuse of $b+s$, a height of $b-s$ and a base length of $q-b-s-a$ (where $a$ is the relatively small length needed to be consider to take the curvature of the quarter circle into account).

From here, we'll now have to start thinking of the image on the Cartesian plane. This means that point $Q$ will be at $(0,0)$, point $B$ will be at $(b,b)$, and point $S$ will be at $(q-s-a, s)$.

The next step is to find a way to express $a$ in terms of $b$ and $s$. The method I ended up going with was using the points we previously determined to calculate the distance between $S$ and $B$:
$$\text{Distance} = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$$
$$\text{Distance} = \sqrt{(q-s-a-b)^2+(s-b)^2}$$
We know that $q=( \sqrt2 b + 1 )b$ and we know that the hypotenuse has a length of $b+s$, therefore we can substitute these in:
$$b+s = \sqrt{(( \sqrt2 b + 1 )b-s-a-b)^2+(s-b)^2}$$
After some quick simplifying and rearranging, we can solve for $a$:
$$a = \sqrt{2}b-2\sqrt{b\cdot s}-s$$

It was around here that I got stuck for a good long while. I couldn't seem to make any more progress trying towards getting a solution algebraically, so instead I decided to graph everything on Desmos and just pick a random value for $b$. Using this I then picked a value for $s$ which generated a graph of closest fit to what was originally pictured. At this point, I had the following equations for the graphs:
$$x^{2}+y^{2}=(( \sqrt2 b + 1 )b)^{2} |\left\{x\ge0\right\}\left\{y\ge0\right\}$$
$$\left(x-b\right)^{2}+\left(y-b\right)^{2}=b^{2}$$
$$\left(x-b\left(\sqrt{2}+1\right)+s+a\right)^{2}+\left(y-s\right)^{2}=s^{2}$$
I decided to start playing around with changing the horizonal translation of the smaller circle. I first tried to graph $x^{2}+\left(y-s\right)^{2}=s^{2}$, but that wasn't too interesting. I then shifted it to the right a little with $\left(x-s\right)^{2}+\left(y-s\right)^{2}=s^{2}$ and that's when the eureka moment hit.

Just from inspection, it looked like the distance between $\left(x-s\right)^{2}+\left(y-s\right)^{2}=s^{2}$ and $\left(x-b\left(\sqrt{2}+1\right)+s+a\right)^{2}+\left(y-s\right)^{2}=s^{2}$ would fit an exact number of circles. So I tried adding another circle with the equation $\left(x-3s\right)^{2}+\left(y-3s\right)^{2}=s^{2}$ and it fit perfectly. After adding the remaining circle in, this is what I had discovered:

All the copies of circle $S$ fit in perfectly. Thus, I was able to quickly determine that radius of the quarter circle must be $8s+a$ (I also realized that the equation I'd been using up to this point for circle $S$ was rather messy and can be neatly simplified to $\left(x-s\right)^{2}+\left(y-7s\right)^{2}=s^{2}$).

This left me with: $8s+a = q$. Substituting in $a = \sqrt{2}b-2\sqrt{b\cdot s}-s$ and $q=( \sqrt2 b + 1 )b$, I had:
$$8s + \sqrt{2}b-2\sqrt{b\cdot s}-s = \left(\sqrt{2}+1\right)b$$
And finally, after one last rearrangement...
$$s=\frac{b}{49}\left(4\sqrt{2}+9\right)$$

The last step
Of course, one final step remains: actually calculating the percentage area remaining:
$$\frac{\frac{\pi}{4}q^{2}-\left(2\pi s^{2}+\pi b^{2}\right)}{\frac{\pi}{4}q^{2}}\cdot100$$
$$=\frac{\frac{\pi}{4}\left(\left(\sqrt{2}+1\right)b\right)^{2}-\left(2\pi\left(\frac{b}{49}\left(4\sqrt{2}+9\right)\right)^{2}+\pi b^{2}\right)}{\frac{\pi}{4}\left(\left(\sqrt{2}+1\right)b\right)^{2}}\cdot100$$
$$=19.09\%$$

Conclusion
To anyone still reading, I just wanted to say thank you. This may be very simple and basic to most people on here, but for me it means so much more than you can imagine. I spent a lot of hours attempting to solve this question, and while I very much appreciated all the help I received here, it was all a fair bit beyond my understanding for it to be of any help to me. I'm just so happy I managed to solve this on my own using a method that I was able to figure out on my own and that made sense to me. I hope this is helpful to someone else out there trying and struggling with some geometry :)