Capacitance of a spherical capacitor

[Guillem_dlc]

Homework Statement

A spherical capacitor is formed by two thin conductive layers, spherical and concentric, of radius $R_1$ and $R_2>R_1$, between which we have placed a dielectric material of relative permittivity $\varepsilon_r$. Knowing that the inner layer has an $Q$ charge, idetermines the capacity of the capacitor and the total energy stored.

Relevant Equations

Gauss Law

When I try to do Gauss, the permeability is not always that of the free space, but it varies: up to a certain radius it is that of the void and then it is the relative one. How can I relate them? I'm trying to calculate the capacity of a spherical capacitor.

The scheme looks like this: inside I have the free space and between the plates of the capacitor I have the dielectric material.

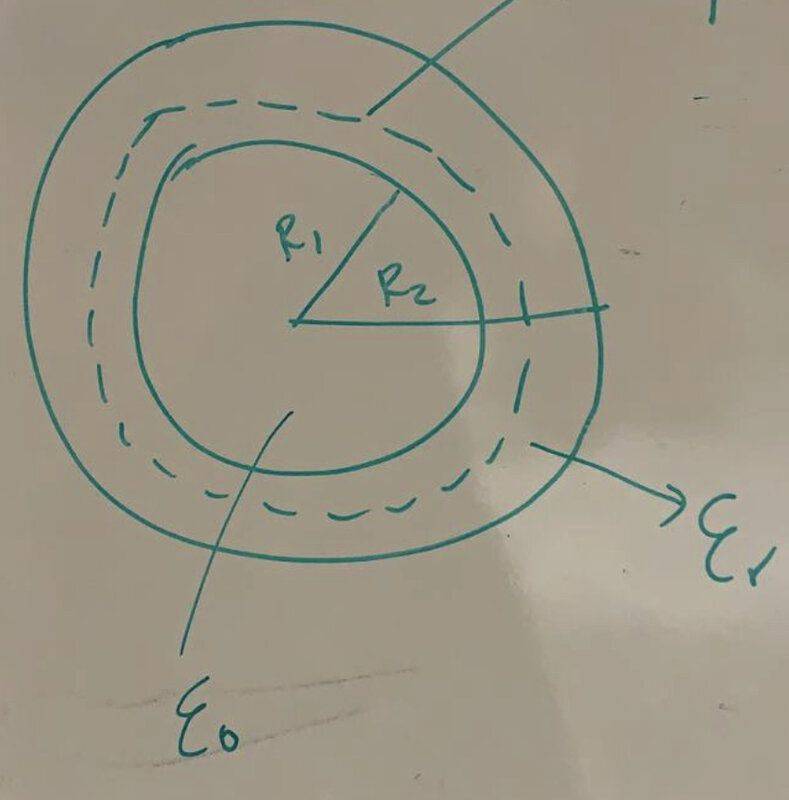
The broken lines represent the Gaussian surface.

 

[hutchphd]

What is the result if it were space ( ε₀) between the spherical shells?

 

[kuruman]

The vacuum doesn't matter because it contains no charge. The capacitor consists of two conducting plates with the space between them filled completely with the dielectric. Use a Gaussian surface completely inside the dielectric. Or you can find the capacitance with no dielectric between the shells and then multiply it by the dielectric constant.

 

[Guillem_dlc]

I think I have the solution. Is that right?
$$\left. \phi =\oint \vec{E}\cdot d\vec{S}=\oint E\cdot dS\cdot \underbrace{\cos 0}_1=E\oint dS=E\cdot S \atop \phi =\dfrac{Q_{enc}}{\varepsilon_0 \varepsilon_r}=\dfrac{Q}{\varepsilon_0 \varepsilon_r}=\dfrac{\sigma \cdot S}{\varepsilon_0 \varepsilon_r} \right\} E\cdot S=\dfrac{\sigma S}{\varepsilon_0 \varepsilon_r}\rightarrow E=\dfrac{\sigma}{\varepsilon_0 \varepsilon_r}=\dfrac{Q}{4\pi R^2 \varepsilon_0}$$
$$C=\dfrac{Q}{V_2-V_1}$$
$$V_2-V_1=-\int_{R_1}^{R_2} \vec{E}\cdot d\vec{l}=-\int_{R_1}^{R_2}E\cdot \overbrace{dl\cdot \cos \theta}^{dR}=-\int_{R_1}^{R_2}\dfrac{Q}{4\pi R^2 \varepsilon_0 \varepsilon_r}dR=\dfrac{Q}{4\pi \varepsilon_0 \varepsilon_r}-\int_{R_1}^{R_2} \dfrac{1}{R^2}dR$$
because $Q$ is constant as it has been transferred to us by an external field/generator. Therefore, it is invariant. $V$ varies due to distance. Then
$$V_2-V_1=\dfrac{Q}{4\pi \varepsilon_0 \varepsilon_r}\left( -\dfrac{1}{R_2}+\dfrac{1}{R_1}\right) \rightarrow C=\dfrac{4\pi \varepsilon_0}{\left( -\frac{1}{R_2}+\frac{1}{R_1}\right)}=\boxed{4\pi \varepsilon_0 \varepsilon_r\dfrac{R_2R_1}{R_2-R_1}}$$

 

[kuruman]

That looks about right.