Electric field between capacitor plates when a dielectric slab is inserted

[Rhdjfgjgj]

Homework Statement

find the Electric field between a capacitor when dielectric is placed between them

Relevant Equations

Eext=E/k(E: field between capacitor plates when no dielectric is put

my sir gave us the above question as homeork,our task to derive why it happens so I couldnt get it right. So today he gave the answer to it. we were also a..sked to find the induced charges on the dielectric surface.
.

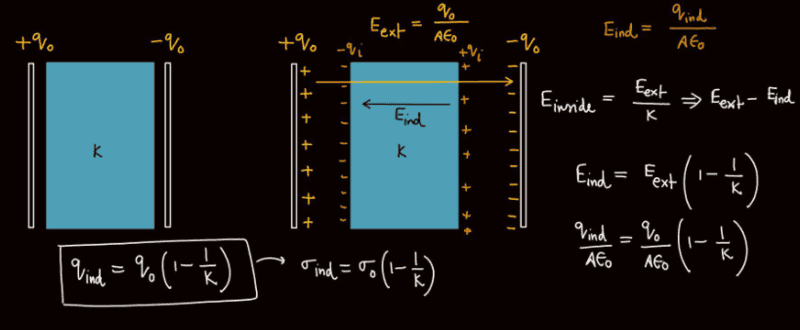
E ext : electric field between capacitor plates when no dielectric was put
E ind : electric field due to induced charges .
E inside : electric field net inside the dielectric
q_i : charge induced

. Here i had an issue with the expression of Eind , Because we are defining it for a point inside the dielectric i felt the denominator must have a factor of K.
Later i went to the internet and referred my books , i found that everywhere it is written same way. What did i think wrong
. please explain

 

[kuruman]

Outside the dielectric there is a uniform electric field $~E_{\text{ext}}.$
Inside the dielectric there is a net uniform electric field $~E_{\text{inside}}.$
The net electric field inside the dielectric is equal to the external field reduced by a factor of $\kappa$:
$~E_{\text{inside}}=\dfrac{E_{\text{ext}}}{\kappa}.$
Why is the field inside the dielectric reduced?
Answer: Because there as induced polarization charge density on the surface of the dielectric as shown in the figure that opposes the external field. Thus the equation $$\begin{align} & E_{\text{inside}}=E_{\text{ext}}-E_{\text{ind.}} \nonumber \\ & \implies E_{\text{ind}}=E_{\text{ext}}-E_{\text{inside}}=E_{\text{ext}}-\frac{E_{\text{ext}}}{\kappa}=E_{\text{ext}}\left(1-\frac{1}{\kappa}\right)=E_{\text{ext}}\left(\frac{\kappa-1}{\kappa}\right).\nonumber \end{align}$$

i felt the denominator must have a factor of K.

What denominator did you feel must have a factor of $\kappa$?

 

[Rhdjfgjgj]

Outside the dielectric there is a uniform electric field $~E_{\text{ext}}.$
Inside the dielectric there is a net uniform electric field $~E_{\text{inside}}.$
The net electric field inside the dielectric is equal to the external field reduced by a factor of $\kappa$:
$~E_{\text{inside}}=\dfrac{E_{\text{ext}}}{\kappa}.$
Why is the field inside the dielectric reduced?
Answer: Because there as induced polarization charge density on the surface of the dielectric as shown in the figure that opposes the external field. Thus the equation $$\begin{align} & E_{\text{inside}}=E_{\text{ext}}-E_{\text{ind.}} \nonumber \\ & \implies E_{\text{ind}}=E_{\text{ext}}-E_{\text{inside}}=E_{\text{ext}}-\frac{E_{\text{ext}}}{\kappa}=E_{\text{ext}}\left(1-\frac{1}{\kappa}\right)=E_{\text{ext}}\left(\frac{\kappa-1}{\kappa}\right).\nonumber \end{align}$$

What denominator did you feel must have a factor of $\kappa$?

The value of Eind . Observe $~E_{\text{ind}}$
is the field due to induced charges at a point inside the dielectric. As taught in electrostatics, permittivity of free space(epsilon not) must be multiplied by the dielectric constant. That's why they must be a k multiplied in the denominator. But it isn't. Why. I looked it up in my books also, all of them have the same way. Why is k not multiplied in the denominator?

 

[kuruman]

What should the correct equation for $~E_{\text{ind}}$ be according to you?

 

[Rhdjfgjgj]

It must be qi/(Ake)

(e : permittivity of free space)
I m sorry, im not able to use the mathematical conventions so I'm typing them down.

 

[kuruman]

You are confusing $~E_{\text{inside}}$ with $~E_{\text{ind}}.$ They are two different things. The black arrow in the figure is not the field inside the dielectric. It is the difference between the external field and the field inside the dielectric.

 

[Rhdjfgjgj]

Nooo. Eind is the field due to induced charges on the dielectric surface. Einside is my field. I know see

 

[Rhdjfgjgj]

With the difference in tone zones, it is becoming difficult to interact. . So I would appreciate it if you could just explain it for me

 

[kuruman]

With the difference in tone zones, it is becoming difficult to interact. . So I would appreciate it if you could just explain it for me

I have no control over the time zones. I explained it above with equations and I will explain it once more with vector diagrams. Look at the figure below drawn to scale.

Top: You have an external field $~E_{\text{ext}}$ which is 3 units.

Middle: You insert a dielectric of $\kappa = 3.$ The field inside the dielectric is $E_{\text{inside}}=\dfrac{E_{\text{ext}}}{\kappa}=\dfrac{3}{3}=1~$unit.

Note that in the region of space where you used to have a field of 3 units to the right without the dielectric, you have 1 unit to the right with the dielectric. How can that be? The answer is below.

Bottom: You must have a field due to the induced charges which is 2 units to the left. The magnitude of that field is $$E_{\text{induced}}=E_{\text{ext}}\left(1-\frac{1}{\kappa}\right)=E_{\text{ext}}\left(1-\frac{1}{3}\right)=\frac{2}{3}E_{\text{ext}}=2~\text{units}.$$What's inside the dielectric is the sum of the external field from the capacitor plates plus the opposing field from the polarized charges on the dielectric surface.

 

[Rhdjfgjgj]

sir all of that is fine my main issue here is that i m confused of the field by the induced charges. . I would have written that expression Eind =qi/(ae), if there were no dielectric. but since i m finding field for a point inside dielectric i think it must be written like qi/(kae)
(e: permittivity of free space , k dielectric constant.

 

[Rhdjfgjgj]

You are confusing $~E_{\text{inside}}$ with $~E_{\text{ind}}.$ They are two different things. The black arrow in the figure is not the field inside the dielectric. It is the difference between the external field and the field inside the dielectric.

and in this post i do understand what you meant by saying that but i m writing the value of E ind independently with induced charges

 

[kuruman]

Eind =qi/(ae), if there were no dielectric.

That shows the origin of your confusion. If there is no dielectric between the plates, there is no induced charge and $E_{\text{ind}}=0$. Take a look at the two equations relating the field inside the the dielectric and the induced field to the field inside the vacuum region $E_{\text{ext}}.$
$$\begin{align} & ~E_{\text{inside}}=\dfrac{E_{\text{ext}}}{\kappa} \nonumber \\
& E_{\text{induced}}=E_{\text{ext}}\left(1-\frac{1}{\kappa}\right).\nonumber
\end{align}$$ If there were no dielectric, the space between the capacitor plates is filled with vacuum which has $\kappa =1$. Then
$$\begin{align} & ~E_{\text{inside}}=\frac{E_{\text{ext}}}{1}= E_{\text{ext}}\nonumber \\
& E_{\text{induced}}=E_{\text{ext}}\left(1-\frac{1}{1}\right)=0\nonumber
\end{align}$$as you might expect when the region where the dielectric used to be becomes vacuum.

 

[Rhdjfgjgj]

That shows the origin of your confusion. If there is no dielectric between the plates, there is no induced charge and $E_{\text{ind}}=0$. Take a look at the two equations relating the field inside the the dielectric and the induced field to the field inside the vacuum region $E_{\text{ext}}.$
$$\begin{align} & ~E_{\text{inside}}=\dfrac{E_{\text{ext}}}{\kappa} \nonumber \\
& E_{\text{induced}}=E_{\text{ext}}\left(1-\frac{1}{\kappa}\right).\nonumber
\end{align}$$ If there were no dielectric, the space between the capacitor plates is filled with vacuum which has $\kappa =1$. Then
$$\begin{align} & ~E_{\text{inside}}=\frac{E_{\text{ext}}}{1}= E_{\text{ext}}\nonumber \\
& E_{\text{induced}}=E_{\text{ext}}\left(1-\frac{1}{1}\right)=0\nonumber
\end{align}$$as you might expect when the region where the dielectric used to be becomes vacuum.

Thanks and even on reading other materials, I found out that since net charge inside the dielectric is zero, it's virtually an empty space between the induced charges

 

[kuruman]

$\dots$ it's virtually an empty space between the induced charges

I don't know what that means but you don't have to explain. Are we done here?

 

[Rhdjfgjgj]

Read it yah we are done