Capacitance of concenctric spheres

[mitleid]

The figure below shows six concentric conducting spheres, A, B, C, D, E, and F having radii R, 2 R, 4 R, 6 R, 7 R, and 9 R, respectively. Spheres B and C are connected by a conducting wire, as are spheres D and E. Determine the equivalent capacitance of this system.

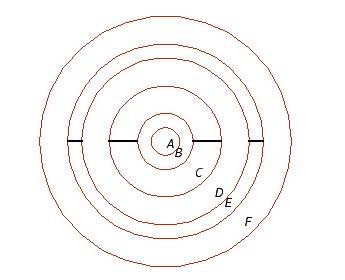
I understand that spheres B and C are equipotentials, as are D and E. Accordingly, they will share their charges with one another.

V = Ke*Q(1/a - 1/b) for a conducting sphere. I plug this into C = Q/V to get C = 1/ke(1/a - 1/b).

My problem is figuring how to knit these radii together into this equation... I guess the spheres which are connected by wire will act as equipotentials, or a capacitor series, and will have equal and opposite charges. This leaves the innermost radius and the outermost to cancel out one another, perhaps...

But I'm trying to find the equivalent capacitance of the system, and I haven't done that with a system of spheres before. In a circuit, Ceq is dependent on the type of connections (series/parallel), here I feel like I'm having to make a few too many assumptions.

I will try solving for Caf, Cbc and Cde, from there I'll have to find Ceq for the total system. Any help would be much appreciated here !

 

[mitleid]

So I think I'm getting closer. I was solving for the same problem with different numbers with R, 2R, 3R, 4R, 5R and 6R. I solved for Caf to get:

1/ke(1/R -1/6R) = 1/ke(5/6R)

Similarly I found Cbc = 1/ke(1/6R) and Cde = 1/ke(1/20R)

From this point I'm really not sure what to do. I went ahead and said Ceq = Caf + Cbc + Cde = 63/60R * 1/ke. The actual answer was 60R/37*1/ke, so I'm doing something essential incorrectly.

Please help!

 

[Depric]

The equation you're searching for is a bit different.

1/Ceq = (1/Cab)+(1/Ccd)+(1/Cef)

You're looking for the capacitance of the system, a series of conductors, while taking into account the irrelevance of certain radii values you see. There are effectively only four conductors in this system: A, the conductor composed of B and C, the conductor composed of D and E, and F. I think for the actual numerical answer, your formula would look something like:

C = (K((1/R - 1/2R)+(1/4R - 1/6R)+(1/7R - 1/9R)))^(-1)

 

[PhDorBust]

I am having similar troubles and I believe that Depric is incorrect. More input would be appreciated.