NickTesla
- 29
- 3
I would like to understand how the Euler constant elevated to fractional exponent gave this result? 958mV someone please!?
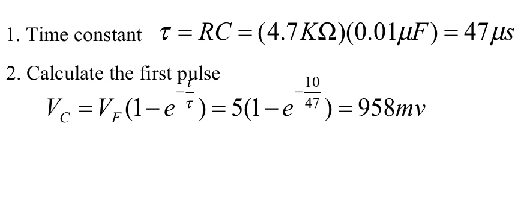
The discussion centers on understanding the calculation of capacitor discharge time using Euler's constant raised to a fractional exponent. The key formula presented is Vc = Vf(1 - e^(-t/T)), where the voltage across the capacitor rises exponentially over time. A specific example is calculated, resulting in a voltage of approximately 958mV, derived from the steps involving e^(-0.212765957). The participants express a need for clearer explanations and resources, particularly in the context of educational materials available in Brazil.
PREREQUISITESStudents, educators, and electrical engineers seeking to deepen their understanding of capacitor discharge calculations and the mathematical principles behind exponential functions.
Svein said:OK. Let us take it in steps:
- \frac{10}{47}= 0.212765957
- e^{-0.212765957}=0.808345302
- 1- 0.808345302=0.191655
- 5 \cdot 0.191655 = 0.958273
Sven Wonderfully Thank you!Svein said:OK. Let us take it in steps:
- \frac{10}{47}= 0.212765957
- e^{-0.212765957}=0.808345302
- 1- 0.808345302=0.191655
- 5 \cdot 0.191655 = 0.958273
Obrigado!NickTesla said:Sven Wonderfully Thank you!











