palaphys
- 266
- 17
- Homework Statement
- A triangular wedge of mass M has a smaller mass m on its top most point. Initially the system is at rest. Considering the fact that the ground is frictionless, analyze the motion of the center of mass of the wedge block system
- Relevant Equations
- P=mv, center of mass= sum of mass * coordinates / sum of all masses, conservation of momentum
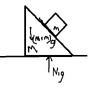
consider this situation. The diagram I have drawn is just after the smaller mass m begins sliding.
So first thing I wanted to do is define my system. Here I have defined my system as "Small mass m+ Larger wedge M".
DOUBT 1: I had a rather silly idea- is it right to consider the "floor" as part of the system? Is that possible in the first place?
okay, now, I drew a free body diagram of the masses to predict how they would behave:-
|
here N_g represents the normal reaction from the ground, and N_1 is the internal normal reaction between the two blocks. I have divided that into two components. So from here, it is clear that the larger mass M is going to move towards the left, with some acceleration.
DOUBT 2: FBD of the "system"
so in addition to these, I am going to draw the FBD of the system as defined earlier:
the forces acting on the system are (M+m)g and the normal force from the ground, N_g.
POINT 1: as there are no external forces operating in the x- direction,
$$p_{ix}= p_{fx} $$
As far as I have learnt, I have learnt that "if there are no external forces acting on a system, the acceleration of the center of mass is 0, i.e the velocity of the center of mass is constant." This implies that the position of the center of mass in the x direction (here) does not change at all.
DOUBT 3:- My main query with this question other than the ones above, is regarding the displacement/ behaviour of the y- coordinates of the center of mass. As per the FBD on the right, the vectors $$ (M+m)g , N_g $$ seem to cancel out each other.
Does this imply that momentum is conserved in the y direction as well? is the CM of the system in rest throughout the motion?
I came to this assumption that it is in rest by considering the equation
$$ F_{ext,y} = (M+m)a_{cm,y} $$, External force here is PROBABLY 0, and under that assumption, a_cm,y becomes zero.
However, when I went through this problem again
$$ Y_cm = (My_1 + my_2)/ (M+m) $$
Differentiating twice,
$$ a_{cm,y} = (Ma_{y1} + ma_{y2} )/ (M+m) $$ (1)
Now going back to the FBD of the the individual blocks,
where $$ a_x1$$ is the acceleration of the larger mass and $$ a_x2 $$ is the acceleration of the smaller mass.
So clearly, $$ a_{cm,x} = 0,$$ using an equation similar to (1) above.
now, it seems to me that $$a_{y1}$$ is zero, as I do not see the larger mass M accelerating along the y direction. However, it is clear that the smaller mass has some acceleration in the y direction.
from this, substituting values in equation (1), the y- component of the acceleration turns out to be non zero. However this contradicts the statement made above.
Where have I gone wrong in this analysis? is the CM stationary along the y plane?
DOUBT 4- I remember reading somewhere that only objects with the same acceleration can be considered as part of a valid system. Is this a myth or is this true?
I would greatly appreciate all help, please do point out mistakes if there are any in this question!
Attachments
Last edited: