Center of Mass Calculation: x-bar, y-bar

[aaronfue]

Homework Statement

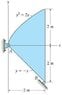
I need to find the center of mass of the given figure attached. I am given the density (7850 kg/m^3) and a thickness of 0.3 cm (not sure where this goes)

Homework Equations

Just some things I need to verify:

When finding the x-bar of the function y=x3 using the equation:

\bar{x}= \frac{∫ \tilde{x} dm}{∫dm},

Is my \bar{x} going to be the x distance(which will just be "x") times x³dm?

Also, will x³ be in the denominator just before "dm"?

If I am also given a density ρ, will that stay in front of each integrand or in front of (\frac{∫ \tilde{x} dm}{∫dm})? And would I calculate the thickness with the \bar{z}?

Is the same process is done for the \tilde{y} or are there differences?

I know this may be a lot but I'd like to make sure of the method.
Thanks!

Homework Statement

Homework Equations

The Attempt at a Solution

 

[Simon Bridge]

dm as the amount of mass in a volume element at point (x,y) with width dx, height dy, and thickness t ... that would be $dm = \rho(x,y) dV = \rho tdxdy$
...that help clarify things?

Of course you can simplify the calculation a lot by understanding it.

 

[rude man]

Homework Statement

I need to find the center of mass of the given figure attached. I am given the density (7850 kg/m^3) and a thickness of 0.3 cm (not sure where this goes)

/b]

I suggest paying very little attention to the (uniform) density and not too much time on the (uniform) thickness ...

 

[Simon Bridge]

I suggest paying very little attention to the (uniform) density and not too much time on the (uniform) thickness ...

Well, me too ... though it comes out in the wash :) It's part of the "you can simplify the calculation a lot by understanding it" thing.

It is also easier to do the integration against y instead of x and part of the integration can be done just by knowing the formula for the area of a triangle - but I don't know how much aaronfue understands vs memorizes equations. Do need to hear from him before we can continue methinks.

 

[rude man]

Well, me too ... though it comes out in the wash :) It's part of the "you can simplify the calculation a lot by understanding it" thing.

It is also easier to do the integration against y instead of x and part of the integration can be done just by knowing the formula for the area of a triangle - but I don't know how much aaronfue understands vs memorizes equations. Do need to hear from him before we can continue methinks.

Big 10-4, Simon. Not having my textbook at the ready right now, I would approach the problem as finding the axis of zero net torque under gravity and arbitrary orientation, in which case integration of a differential wedge dθ might make sense. As an EE I'll probably pass on doing the actual work, so talk's cheap!

 

[Simon Bridge]

Who needs textbooks when you have google ;)

 

[rude man]

Who needs textbooks when you have google ;)

True, true. So chalk it up to indolence on my part ...