Center of mass, moment of inertia for x = y^2 and y = x - 2 with density d = 3x

[VinnyCee]

Here is the problem:

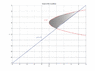
A region is defined as being bounded by the parabola x = y^2 and the line y = x - 2.

The density of this region is \delta = 3x.

a) Find the center of mass.

b) Find the moment of inertia about the y-axis.

c) Find the radius of gyration about the y-axis.

Here is what I have:

M = \int_{-1}^{2}\int_{y^2}^{y + 2}\;3x\;dx\;dy = \frac{108}{5}

M_{x} = \int_{-1}^{2}\int_{y^2}^{y + 2} 3xy\;dx\;dy = \frac{135}{8}

M_{y} = \int_{-1}^{2}\int_{y^2}^{y + 2} 3x^2\;dx\;dy = \frac{1269}{28}

\bar{x} = \frac{\frac{1269}{28}}{\frac{108}{5}} = \frac{235}{112}\;\;and\;\;\bar{y} = \frac{\frac{135}{8}}{\frac{108}{5}} = \frac{25}{32}

I_{y} = \int_{-1}^{2}\int_{y^2}^{y + 2} x^2 \left(3x\right)\;dx\;dy = 110.7

R_{y} = \sqrt{\frac{110.7}{\frac{108}{5}}} \approx 2.26

Does this look correct?

 

[HallsofIvy]

I get what you do for M but 153/8 rather than 135/8 forMx. I get completely different answer for the others- but I may have tried to do them too fast.

 

[dextercioby]

I don't know what Halls did,but all your calculations are perfect.I double checked them with Maple...


Daniel.