Centre of mass of a hollow pyramid

[subzero0137]

Question: Calculate the centre of mass of a uniform, square-based pyramid of height H and base length B (taking the centre of the base as the origin). Hence, or otherwise, derive an expression for the centre of mass of such a pyramid with a pyramid-shaped hollow cavity (of height h and base length b) inside, as shown:

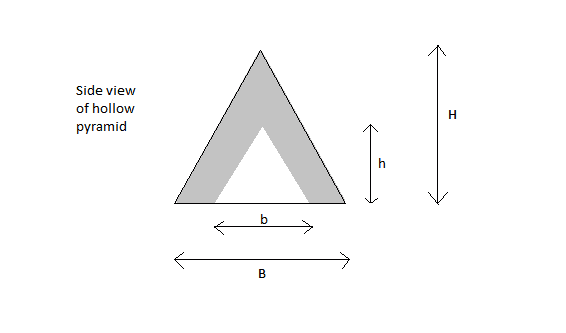
Key equation: $$CoM = \frac {\int z \, dm} {\int\, dm} = \frac {\int zρ \, dV} {\int\, dV}$$Attempt: By symmetry, the CoM must lie on the line connecting the apex and the centre of the base, let's call this the z axis. By considering horizontal slices parallel to the base, of thickness dz and area xy, $dV = xydz = \frac {B^2} {H^2} (H - z)^2 dz,$ therefore

$$CoM = \frac {\int_0^H zρ \frac{B^2}{H^2} (H - z)^2 \, dz} {\int_0^H ρ \frac{B^2}{H^2} (H - z)^2 \, dz} = \frac {H} {4}$$

However I don't know how to get an expression for the hollow/cavity pyramid. I was told to treat the hollow as being a pyramid of negative mass but I'm unsure as to how to go from there.

 

[mfb]

Center of masses add linearly (e.g. as vectors). You can treat the hollow pyramid as made out of two parts, a full pyramid and a smaller full pyramid with negative density, calculate the center of mass for both separately, then combine them to one object that looks like the pyramid you want.

 

[subzero0137]

Center of masses add linearly (e.g. as vectors). You can treat the hollow pyramid as made out of two parts, a full pyramid and a smaller full pyramid with negative density, calculate the center of mass for both separately, then combine them to one object that looks like the pyramid you want.

So the centre of mass for the smaller pyramid would be $\frac {h} {4}$, but I get this result regardless of the sign in front of density so I'm still confused. How would I combine them into one object, by simply adding them? So $CoM = \frac {H} {4} + \frac {h} {4}$?

 

[PeroK]

So the centre of mass for the smaller pyramid would be $\frac {h} {4}$, but I get this result regardless of the sign in front of density so I'm still confused. How would I combine them into one object, by simply adding them? So $CoM = \frac {H} {4} + \frac {h} {4}$?

Physically, you are subtracting the smaller pyramid from the larger pyramid. Not adding it.

Another way to look at it is that if S is the hollow pyramid, P the big pyramid and p the small pyramid, then

$P = S + p$

This avoids the concept of negative densities.

 

[subzero0137]

Physically, you are subtracting the smaller pyramid from the larger pyramid. Not adding it.

Another way to look at it is that if S is the hollow pyramid, P the big pyramid and p the small pyramid, then

$P = S + p$

This avoids the concept of negative densities.

So it would be $CoM = \frac {H} {4} - \frac {h} {4}$? But this seems counter intuitive because it's shifting the CoM closer to the base whereas most of the mass is near the top of the hollow pyramid?

 

[PeroK]

So it would be $CoM = \frac {H} {4} - \frac {h} {4}$? But this seems counter intuitive because it's shifting the CoM closer to the base whereas most of the mass is near the top of the hollow pyramid?

Are the masses of the respective components important?

 

[subzero0137]

Are the masses of the respective components important?

I'm assuming yes, or it is the volume that is important? I'm struggling to understand why it would shift down and not up if it is hollow from the bottom?

 

[PeroK]

I'm assuming yes, or it is the volume that is important? I'm struggling to understand why it would shift down and not up if it is hollow from the bottom?

The vector quantity is actually the product of a mass by its centre of mass. E.g. if you have two masses, mass $M$ at the origin and mass $m$ a distance $x$ from the origin, then the centre of mass of the system is $\frac{mx}{M +m}$.

By your method it would always be $x$, regardless of the masses.

 

[PeroK]

Ps The general case for a system of masses is:

$\vec{r} = \frac{\sum m_i \vec{r_i}}{\sum m_i}$

Which, of course, for a continuous mass distribution leads to the integral form you quoted in your original post.

And, if we let $m = \sum m_i$ then we have:

$m\vec{r} = \sum m_i \vec{r_i}$

Which is the vector sum of moments (mass times centre of mass).

 

[subzero0137]

The vector quantity is actually the product of a mass by its centre of mass. E.g. if you have two masses, mass $M$ at the origin and mass $m$ a distance $x$ from the origin, then the centre of mass of the system is $\frac{mx}{M +m}$.

By your method it would always be $x$, regardless of the masses.

Okay, I think the equation makes sense as you put it. Just to confirm, it is H/4 - h/4 in this case, right? I think I'm just having a hard time understanding it intuitively because from the diagram it looks like the pyramid is heavier at the top in hollow case.

 

[PeroK]

Okay, I think the equation makes sense as you put it. Just to confirm, it is H/4 - h/4 in this case, right? I think I'm just having a hard time understanding it intuitively because from the diagram it looks like the pyramid is heavier at the top in hollow case.

No..The equation must involve the mass of each component. You can't simply add centre of mass vectors. See my posts above.

 

[Orodruin]

Key equation: $$CoM = \frac {\int z \, dm} {\int\, dm} = \frac {\int z\rho \, dV} {\int \rho\, dV}$$

Let's start from here to explain what the others are saying and how it affects your situation (I have added a missing $\rho$ in your denominator).

In general, the structure of both your numerator and denominator are the same so let us work with a more general integral of the form
$$
I[f] = \int \rho(\vec x) f(\vec x) dV,
$$
where $f(\vec x) = 1$ in the denominator and $f(\vec x) = \vec x$ in the numerator ($z$ in the case you are just interested in the vertical position of the CoM). Your CoM expression is now
$$
\vec x_{\rm CoM} = \frac{I[\vec x]}{I[1]}.
$$
Let us now name some volumes, call the space occupied by the hollow pyramid $\Omega_1$, the space of the hole $\Omega_2$ and the combined pyramid (i.e., without the hole) $\Omega = \Omega_1 + \Omega_2$. Since you only have non-zero density in $\Omega_1$, it holds that
$$
I[f] = \int_{\Omega_1} \rho f \, dV.
$$
However, it is easier for you to compute the integral over the full $\Omega$ and the integral over $\Omega_2$ is just the same as a rescaling of the $\Omega$ integral as they are both full pyramids. You therefore note that
$$
\rho \int_{\Omega} f\, dV = \int_{\Omega_1} \rho f\, dV + \int_{\Omega_2} \rho f\, dV = I[f] + \rho \int_{\Omega_2} f\, dV.
$$
Solving for $I[f]$, we find that
$$
I[f] = \int_{\Omega} \rho f\, dV - \int_{\Omega_2} \rho f\, dV.
$$
Note here how the first term is the term you wold have for the denominator/numerator if you were computing the CoM for the full pyramid and the second the term you would have for the denominator/numerator if you were computing the CoM for the hollow part. Also note that you have to do the subtraction separately for the numerator and for the denominator.

Since your density is constant, you can also take $\rho$ out of your integrals and cancel them, then you will use the volumes rather than the masses, but you must use them separately in the numerator/denominator.

 

[subzero0137]

Let's start from here to explain what the others are saying and how it affects your situation (I have added a missing $\rho$ in your denominator).

In general, the structure of both your numerator and denominator are the same so let us work with a more general integral of the form
$$
I[f] = \int \rho(\vec x) f(\vec x) dV,
$$
where $f(\vec x) = 1$ in the denominator and $f(\vec x) = \vec x$ in the numerator ($z$ in the case you are just interested in the vertical position of the CoM). Your CoM expression is now
$$
\vec x_{\rm CoM} = \frac{I[\vec x]}{I[1]}.
$$
Let us now name some volumes, call the space occupied by the hollow pyramid $\Omega_1$, the space of the hole $\Omega_2$ and the combined pyramid (i.e., without the hole) $\Omega = \Omega_1 + \Omega_2$. Since you only have non-zero density in $\Omega_1$, it holds that
$$
I[f] = \int_{\Omega_1} \rho f \, dV.
$$
However, it is easier for you to compute the integral over the full $\Omega$ and the integral over $\Omega_2$ is just the same as a rescaling of the $\Omega$ integral as they are both full pyramids. You therefore note that
$$
\rho \int_{\Omega} f\, dV = \int_{\Omega_1} \rho f\, dV + \int_{\Omega_2} \rho f\, dV = I[f] + \rho \int_{\Omega_2} f\, dV.
$$
Solving for $I[f]$, we find that
$$
I[f] = \int_{\Omega} \rho f\, dV - \int_{\Omega_2} \rho f\, dV.
$$
Note here how the first term is the term you wold have for the denominator/numerator if you were computing the CoM for the full pyramid and the second the term you would have for the denominator/numerator if you were computing the CoM for the hollow part. Also note that you have to do the subtraction separately for the numerator and for the denominator.

Since your density is constant, you can also take $\rho$ out of your integrals and cancel them, then you will use the volumes rather than the masses, but you must use them separately in the numerator/denominator.

Thanks, I managed to obtain the follow expression for the CoM of the pyramid with the cavity:
$$CoM = \frac {B^2 H^2 - b^2 h^2} {4(B^2 H - b^2 h)}$$

Is this correct?

 

[mfb]

Looks good.