Calculating Center of Mass in NH3 Molecule

[JessicaHelena]

Homework Statement

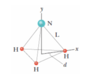
In the ammonia (NH3) molecule of the figure, the three hydrogen (H) atoms form an equilateral triangle, with the center of the triangle at distance d = 9.40 ✕ 10^−11 m from each hydrogen atom. The nitrogen (N) atom is at the apex of a pyramid, with the three hydrogen atoms forming the base. The nitrogen-to-hydrogen atomic mass ratio is 13.9, and the nitrogen-to-hydrogen distance is L = 10.14 ✕ 10^−11 m.

(a) What is the x coordinate of the molecule's center of mass?

(b) What is the y coordinate of the molecule's center of mass?

Homework Equations

x_cm = sum of (m*x)/M
(same for y)

The Attempt at a Solution

(a) I'm not quite sure how to deal with the two hydrogens towards the negative x-axis — they're not exactly on the axis at all.

(b) None of the H's have any y values, so I did 13.9*sqrt(L^2-d^2)/(13.9+3*1) where 3*1 accounted for the masses of the three H's, but apparently that answer is wrong, and I've no idea why it is. (I got 1.137*10^-(10).)

 

[Charles Link]

You need to work out the geometry better for part (a). This is really just a geometry problem, with an equilateral triangle, and the origin (x=0) is at the centroid of that equilateral triangle. This can be readily shown to be the x-center of mass, and we can show that once we have the coordinates. $\\$ (Edit: Go to the bottom, and read that part first. Looking over what you did, you have already done most of what the problem asks for). $\\$ (They really should call their y-direction z, and the plane of the 3 hydrogen atoms should be the x-y plane, but I think they were trying to make it overly simple). I would recommend you make this change, and compute the location of the coordinates of the vertices of an equilateral triangle in the x-y plane, when the centroid is at $(x,y)$ of $(d,0 )$, and compute $(x,y)$ for the other two vertices. Then we can show with a little arithmetic that the center of mass in the x-y plane is at (0,0). Otherwise, we can simply assume that the x-center of mass is $x=0$ as defined in this problem, but that makes it almost too easy.$\\$ $\\$ The location of the center of mass in the $y$ direction is very readily computed. They give you the hypotenuse distance, but you need to compute the distance $d$ from the centroid of the equilateral triangle to the hydrogen atom(s). (Edit: They give you that distance $d$. That makes it very easy). Once you have that, it is a simple matter using the Pythagorean theorem to compute the y-height of the nitrogen atom. Computing the y-center of mass then follows with a very simple equation. (Edit: And I see you did that. Very good ).$\\$ Edit: Looking over your work for part (b), it looks correct. Check your arithmetic=I get a very different answer.

 

[JessicaHelena]

@Charles Link
for the x_cm, I too thought that it would be 0, but the answer is 9.40 ✕ 10^−11 m... Do you have any idea why this could be?

 

[Charles Link]

@Charles Link
for the x_cm, I too thought that it would be 0, but the answer is 9.40 ✕ 10^−11 m... Do you have any idea why this could be?

That is incorrect. The way they drew their coordinate system, they have the (x-coordinate of the) center of mass at $x=0$. (The center of mass (x-coordinate) for the 3 hydrogen atoms is at $x=0$ with the nitrogen atom directly above it ). They did not put the origin of x at the position of the hydrogen atom that is located on the x-axis. The textbook you have needs to be more accurate. $\\$ In any case, please try your arithmetic again for part (b). You should be able to get the same answer that I did.

 

[JessicaHelena]

Oh yes, I did — (b)'s alright now. Thank you.