- #1
hover
- 343
- 0
Hello,
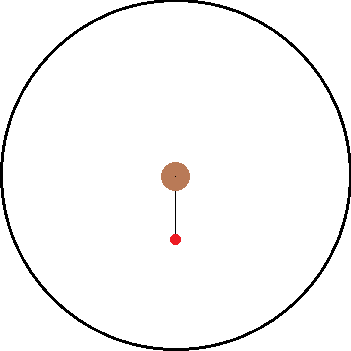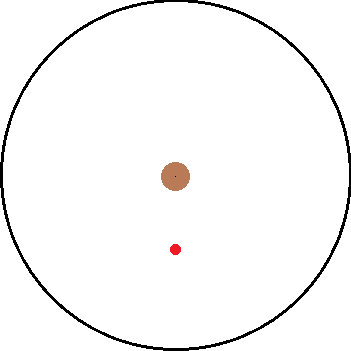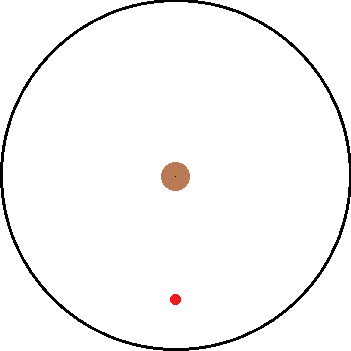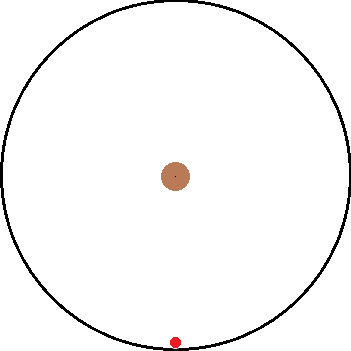
I've been thinking about inertial and non inertial reference frames. A common example is non rotating reference frame vs a rotating reference frame. As illustration, I have attached two images below. The left is the inertial frame and the right is the non inertial frame.
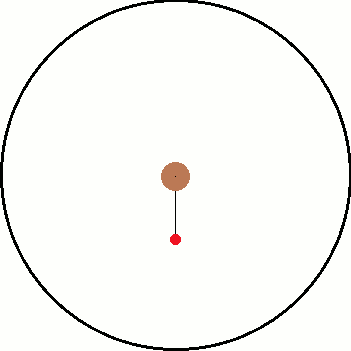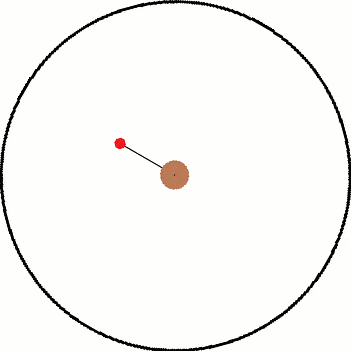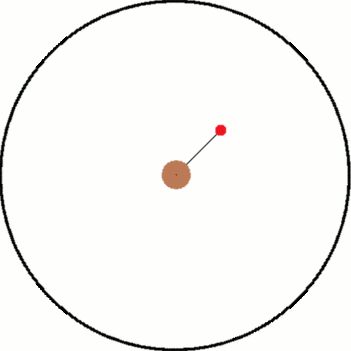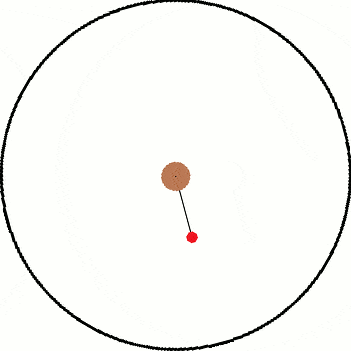
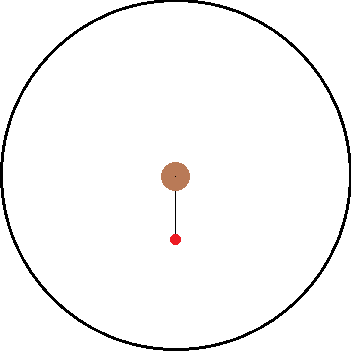
Both images have the same objects in them and only differ by their frame of reference. Inside both frames there is a red ball that is attached to a black string which is connected to the center. In the inertial frame, the ball is being swung around the center as the string provides a centripetal force. In the non inertial frame, the ball "feels" a force pulling it away from the center.
Nothing too special so far. I then thought of asking the following question:
If the string were to break, how long would it take for the ball to reach the outer black circle?
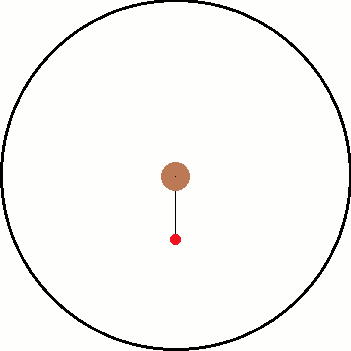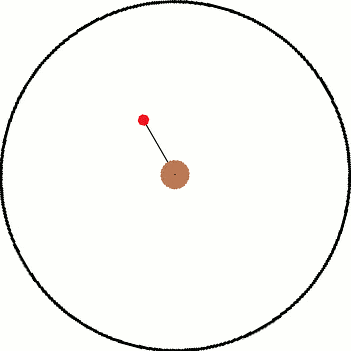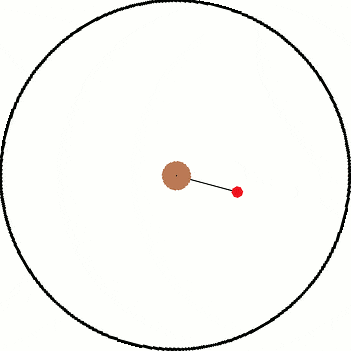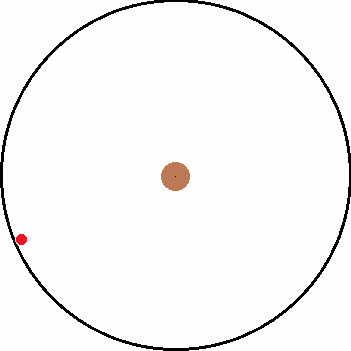
Now classically, I know that both frames are going to arrive at the same answer. However, the fun comes from seeing how both frames try to arrive at that same answer. The easier of the two frames to deal with is the inertial frame since there are no forces present once the string breaks. Using the image below, I will derive the amount of time it takes:
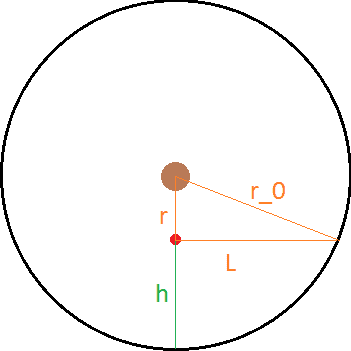
Assuming that the ball is rotating around the center with an angular speed of [itex]\omega[/itex] and at a distance of [itex]r[/itex] from the center, the velocity of the ball when the string breaks is:
[itex]v = r\omega[/itex]
The distance the ball will travel before it reaches the black circle is [itex]L[/itex]. Now [itex]L[/itex] is a variable dependent on [itex]r[/itex] and [itex]r_0[/itex] (the radius of the circle). Using the Pythagorean Theorem:
[itex]r^2 + L^2 = r_0^2[/itex]
[itex]L^2 = r_0^2-r^2[/itex]
[itex]L = \sqrt{r_0^2-r^2}[/itex]
So now we can determine the amount of time it takes to be:
[itex]t_0 = \frac{L}{v} = \frac{\sqrt{r_0^2-r^2}}{r\omega}[/itex]
It's a pretty clean result.
Now is the more interesting but complex scenario. How does the non inertial frame go about calculating [itex]t_0[/itex]? I tried to think about it but it starts to get dicey:
[itex]F = m*r*\omega^2[/itex]
[itex]a = r*\omega^2[/itex]
The force pulling the ball down isn't a constant because it is dependent on [itex]r[/itex] which is always changing the second the string breaks. I'm not quite sure how to handle the non inertial problem at this point. I feel that maybe the problem could be answered by trying to setup a DE but I am too rusty on such things. The only thing I do know is that however the non inertial problem arrives at a time, it must equal the value of the inertial frame.
Interesting food for thought to say the least.
I've been thinking about inertial and non inertial reference frames. A common example is non rotating reference frame vs a rotating reference frame. As illustration, I have attached two images below. The left is the inertial frame and the right is the non inertial frame.
Both images have the same objects in them and only differ by their frame of reference. Inside both frames there is a red ball that is attached to a black string which is connected to the center. In the inertial frame, the ball is being swung around the center as the string provides a centripetal force. In the non inertial frame, the ball "feels" a force pulling it away from the center.
Nothing too special so far. I then thought of asking the following question:
If the string were to break, how long would it take for the ball to reach the outer black circle?
Now classically, I know that both frames are going to arrive at the same answer. However, the fun comes from seeing how both frames try to arrive at that same answer. The easier of the two frames to deal with is the inertial frame since there are no forces present once the string breaks. Using the image below, I will derive the amount of time it takes:
Assuming that the ball is rotating around the center with an angular speed of [itex]\omega[/itex] and at a distance of [itex]r[/itex] from the center, the velocity of the ball when the string breaks is:
[itex]v = r\omega[/itex]
The distance the ball will travel before it reaches the black circle is [itex]L[/itex]. Now [itex]L[/itex] is a variable dependent on [itex]r[/itex] and [itex]r_0[/itex] (the radius of the circle). Using the Pythagorean Theorem:
[itex]r^2 + L^2 = r_0^2[/itex]
[itex]L^2 = r_0^2-r^2[/itex]
[itex]L = \sqrt{r_0^2-r^2}[/itex]
So now we can determine the amount of time it takes to be:
[itex]t_0 = \frac{L}{v} = \frac{\sqrt{r_0^2-r^2}}{r\omega}[/itex]
It's a pretty clean result.
Now is the more interesting but complex scenario. How does the non inertial frame go about calculating [itex]t_0[/itex]? I tried to think about it but it starts to get dicey:
[itex]F = m*r*\omega^2[/itex]
[itex]a = r*\omega^2[/itex]
The force pulling the ball down isn't a constant because it is dependent on [itex]r[/itex] which is always changing the second the string breaks. I'm not quite sure how to handle the non inertial problem at this point. I feel that maybe the problem could be answered by trying to setup a DE but I am too rusty on such things. The only thing I do know is that however the non inertial problem arrives at a time, it must equal the value of the inertial frame.
Interesting food for thought to say the least.