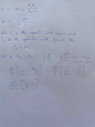Change in energy stored in a spherical Capacitor

[ssarpal]

Homework Statement

An isolated Capacitor is made of a solid conducting sphere of radius R1 and charge +Q surrounded by a conducting spherical shell of inner radius R2 and charge -Q. Initially, the gap between the sphere and the shell has vacuum. Later it is filled with a liquid which has a dielectric constant, K.

For diagram, refer to Fig 8.6 in Section 8.1 Capacitors and Capacitance of University Physics Vol 2 here ...
https://openstax.org/books/university-physics-volume-2/pages/8-1-capacitors-and-capacitance

By how much does the energy change when the liquid is added? Does it increase or decrease?

Relevant Equations

From the same section of the book, eq 8.4 gives the Capacitance of a sphere,

𝐶 = 𝑄/𝑉 = 4𝜋𝜀0 * 𝑅1𝑅2/(𝑅2−𝑅1)

Energy stored in a Capacitor is

U = Q^2/2C

I have attached my solution.

Unfortunately, after plugging in the values, my answer is 4 times more than the expected one. What am I missing?

 

[kuruman]

Your solution looks OK. You probably made a calculation error. Please post your substitutions, final answer and the answer you were told is correct.

 

[ssarpal]

The answer that we were told turned out to be incorrect. Thanks.