Changing cross-sectional area effect on induced current

[Casalino F]

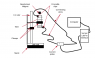
Recently I did an experiment where I dropped a magnet through a tube that was surrounded by a coil, and I hoped to investigate a factor that would affect the current induced (Faraday's law). I chose to study the effect that changing the cross-sectional area of the wire had on the induced current. Due to limited resources, we augmented the cross-sectional area by adding more wires in parallel, instead of simply using thicker wires.
My hypothesis was that as you increase the cross-sectional area, the resistance decreases, which would result in a higher peak current. However, the data that I collected showed exactly the opposite. Instead of a linear increase that I expected, I got a steady decrease in current as I increased the cross-sectional area. It would seem that I have somehow inadvertently increased the resistance of the wires, which would result in the decreasing current. I have loads of different theories on what could have been the cause of this error, but I managed to show that each one of these wasn't the real cause.

Below are the possible sources of error that I eliminated:
- Lenz's law (The magnetic field created by the induced current goes in the opposite direction of the original one and causes some resistance. The more current passing through, the greater this opposing magnetic field will be. Perhaps what happened was that as we increased the cross-section, the current increased, which caused a bigger opposing magnetic field, and overall resulted in more resistance and less current. This theory, however, isn’t plausible because for the opposing field to have been big enough to ‘overpower’ the original one, we would have needed higher currents to produce such as field)
- I also managed to eliminate any possible source of error which could have derived from the current probe used or the crocodile clips.
- Another thing which affects the current passing through is the length of the wire. By adding more coils, one could say that you are actually adding length to the overall wire, but this is only true if the wires are in series. We put the wires in parallel so we never changed the distance of the individual wires
- Sidenote: We also didn't change the diameter of the tube, the length of the wires, the individual cross-sectional areas, the strength of the magnet, the velocity at which the magnet passed through the tube etc.
- Related Equations and laws: Ohm's law, Faraday's law, Lenz's law.

Does anyone else have any ideas? The results of the experiment basically go against all the physical laws I can think of, and I would really appreciate your help. Thanks again.

[NOPARSE] physicsgraphv.2.png [/NOPARSE]

 

[mfb]

A sketch or an image and measurement results would help. You can attach images via the "upload" button.

 

[rude man]

OK, assume the magnet's field across the coil looks like φ(t) = kt as the magnet approaches the coil at t=0.
So during that time we can solve the equation iR + L di/dt = k
with L the coil inductance which is a weak function of wire diameter as long as wire dia. << coil dia. , giving
i(t) = (k/R)[1 - exp(-Rt/L)]. So the current tends to k/R for times t >> L/R.

Putting some numbers in, for a 3 cm. dia. coil L ~ 1.5e-7H, R ~ 1 ohm so L/R ~ 1.5e-7s or 0.15us which is very fast, faster than any fall times so you can assume current easily tops out at i = k/R before decreasing again.
So so far it looks like current should basically go up as R goes down.

However, as current increases the magnet's fall is slowed down more by the coil flux opposing the magnet flux, which makes k smaller (it takes longer for the flux to reach its maximum value). Then k/R might decrease even though R decreases. (This slow-down effect is a favorite lecture demo in e-m courses).

This is one of probably several possible scenarios so who knows for sure.

 

[Casalino F]

A sketch or an image and measurement results would help. You can attach images via the "upload" button.

 

[Casalino F]

OK, assume the magnet's field across the coil looks like φ(t) = kt as the magnet approaches the coil at t=0.
So during that time we can solve the equation iR + L di/dt = k
with L the coil inductance which is a weak function of wire diameter as long as wire dia. << coil dia. , giving
i(t) = (k/R)[1 - exp(-Rt/L)]. So the current tends to k/R for times t >> L/R.

Putting some numbers in, for a 3 cm. dia. coil L ~ 1.5e-7H, R ~ 1 ohm so L/R ~ 1.5e-7s or 0.15us which is very fast, faster than any fall times so you can assume current easily tops out at i = k/R before decreasing again.
So so far it looks like current should basically go up as R goes down.

However, as current increases the magnet's fall is slowed down more by the coil flux opposing the magnet flux, which makes k smaller (it takes longer for the flux to reach its maximum value). Then k/R might decrease even though R decreases. (This slow-down effect is a favorite lecture demo in e-m courses).

This is one of probably several possible scenarios so who knows for sure.

Thank you very much!

 

[mfb]

You had a wire with a cross section of less than $1 \mu m^2$? That looks very thin. Why is the relation (number of wires) to (cross section) not linear?

Can you show a sketch of the setup?

The falling speed of the magnet would also be interesting - was it notably different between the different runs?

 

[Casalino F]

You had a wire with a cross section of less than $1 \mu m^2$? That looks very thin. Why is the relation (number of wires) to (cross section) not linear?

Can you show a sketch of the setup?

The falling speed of the magnet would also be interesting - was it notably different between the different runs?

Yes, the wires were extremely thin and to increase the cross-sectional area we simply put individual wires in parallel (Each individual wire had a diameter of 0.6micrometers). I tried re-calculating the cross-sectional areas, and I got the same results. (for 2 wires, the diameter would be 1.2μm^2 and therefore the radius would be 0.6μm^2 and if you do radius^2 x Pi, you would get 1.13μm^). I agree though, the relationship between cross section and number of wires should be linear...
We always dropped the magnet from the same height (therefore the magnet always accelerated by the same amount), and hence, the velocity of the magnet was kept as a constant. Below I have put a diagram of the setup. Thanks again for your help.

 

[mfb]

Two wires have twice the cross section as one wire, not 4 times. If you put them next to each other the size of one dimension increases by a factor of 2 but the other one does not increase.

We always dropped the magnet from the same height (therefore the magnet always accelerated by the same amount), and hence, the velocity of the magnet was kept as a constant.

The magnet slows down in your setup. Its speed can be different, if the magnetic field generated by the coil is strong enough to have an effect.

Did you also record how long the current lasted?

 

[Casalino F]

Two wires have twice the cross section as one wire, not 4 times. If you put them next to each other the size of one dimension increases by a factor of 2 but the other one does not increase.The magnet slows down in your setup. Its speed can be different, if the magnetic field generated by the coil is strong enough to have an effect.

Did you also record how long the current lasted?

I just went over the times, and indeed, I found that the magnet did slow down (the time the current was being induced increased as you can see from the attached image). I had originally thought that the opposing magnetic field wouldn't have been big enough to "overpower" the original one because the currents weren't big enough, but I didn't think about checking the times. Thank you very much!

 

[mfb]

The average in the last two lines is larger than the largest entry.

 

[Casalino F]

The average in the last two lines is larger than the largest entry.

Yes I double checked the averages and in fact I accidentally divided the sum of the trials by five instead of six in the excitement... For 8 wires the average should be 0.2603sec, and for 10 wires the average should be 0.2516sec. Thanks again!