- #1
LCSphysicist
- 645
- 161
- Homework Statement
- All below
- Relevant Equations
- All below
I am trying to figure out why the relativity don't get in the doppler effect, that is, why can't we apply the "galileo transformations" in doppler effect?
OBS: i am not saying about doppler effect relativistic (using Lorentz transformation)
In another words, i am moving in direction to a source with velocity v, we use the first case below.
But if i imagine that actually the font is going in my direction, as classical mechanics allows, i could try to use the second case.
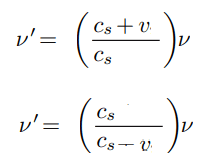
OBS: i am not saying about doppler effect relativistic (using Lorentz transformation)
In another words, i am moving in direction to a source with velocity v, we use the first case below.
But if i imagine that actually the font is going in my direction, as classical mechanics allows, i could try to use the second case.