Changing the interval of integration

[Amaelle]

Homework Statement

look at the image

Relevant Equations

Green theorem

Greetings Dear community!

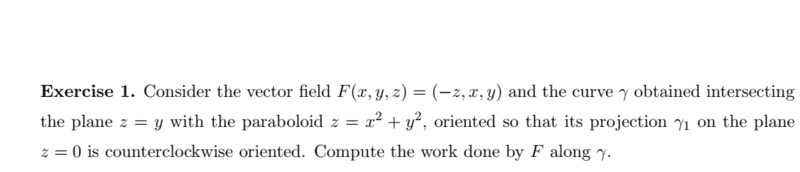
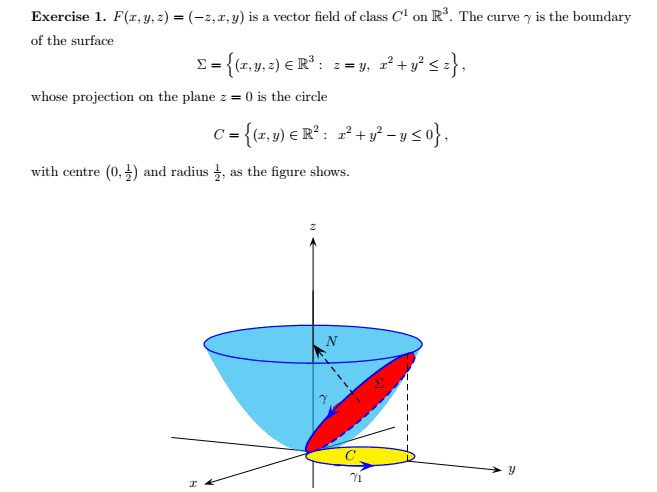
Here is the solutions using two different methods: the first method is the Green theorem and the second is the simple path integration method:


My question is why they integrate over [0.2pi] in the path integration method while they integrate within [0. pi] in the green method (I do agree with it)?

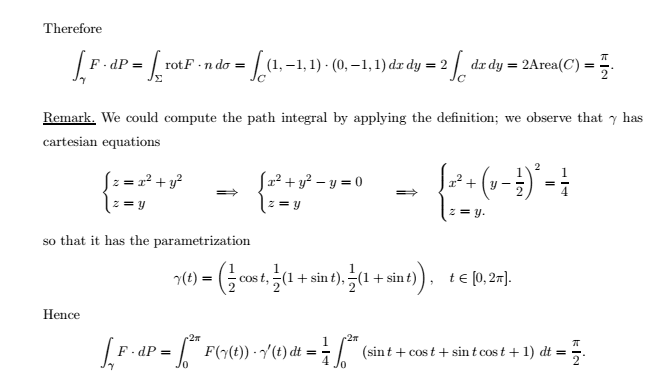
thank you!

 

[Orodruin]

They don’t seem to be using any parametrization at all when applying Stokes’ theorem.

The value of an integral does not depend on the parametrization. You could have picked a parameter taking values in $[-200.5,\pi]$ and you would get the same result (although a bit more annoying expressions for the differentials).

 

[Amaelle]

for the stock theroem they calculate the surface by integrating from [0 ,pi], this is why i don't understand why they didn't do the same for the path integral