Changing the order of a triple integration

[paraboloid]

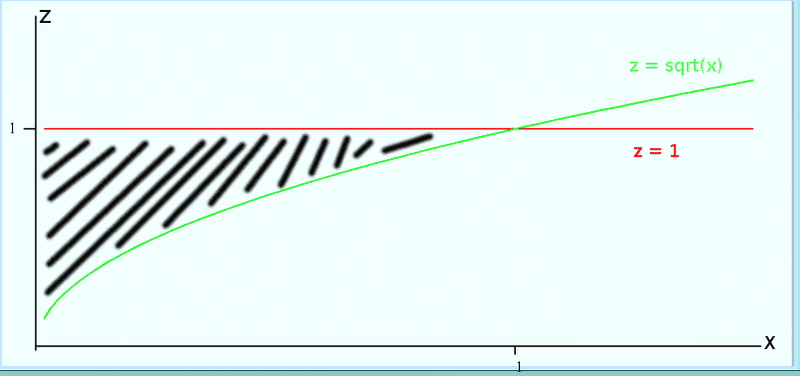
I'm given this definite integral:
$\int_0^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)dzdydx$

I need to change the order to dydxdz, but I'm stuck trying to get the limits of integration wrt y.

$\int_0^{1}\int_{x^2}^{0}\int_{}^{}f(x,y,z)dydzdx$

How do I find the limits of y?

 

[Mark44]

Just look at the original iterated integral to see the region over integration occurs.

z = 0 to z = 1 - y
y = sqrt(x) to y = 1
x = 0 to x = 1.

Sketch that region and it will help you determine the limits of integration for a different order of integration.