AAMAIK
- 45
- 0
- TL;DR
- I want to understand intuition behind the Jacobian matrix proof
Suppose we have a region R in the x-y plane and divide the region into small rectangles of area dxdy. If the integrand or the limits of integration were to be simplified with the introduction of new variables u and v instead of x and y, how can I supply the area element in the u-v system in the same x-y plane?
To generalise let u and v are both functions of x and y. By Holding y=y0 constant and changing x from x0 to x0+Δx this would result in changes in u and v.
Δu1≈ (∂u/∂x)Δx The partial derivatives evaluated at (x0,y0)
Δv1≈ (∂v/∂x)Δx
will serve as a good approximation to u and v at (x0+Δx,y0)
Similarly, holding x=x0+Δx and changing y from y0 to y0+Δy this will result in changes
Δu2≈ (∂u/∂y)Δy
Δv2≈ (∂v/∂y)Δy The partial derivatives evaluated at (x0+Δx,y0)
Holding y=y0+Δy and changing x from x+Δx to x0 will result in changes
Δu3≈ -(∂u/∂x)Δx
Δv3≈ -(∂v/∂x)Δx The partial derivatives evaluated at (x0+Δx,y0+Δy)
Holding x=x0 and changing y from y0+Δy to y0 will result in changes
Δu4≈ -(∂u/∂y)Δy
Δv4≈ -(∂v/∂y)Δy The partial derivatives evaluated at (x0,y0+Δy)
What I did was look at how u and v changed with each edge of the rectangle. But I cannot seem to get how the above fits together into forming the area in the uv system
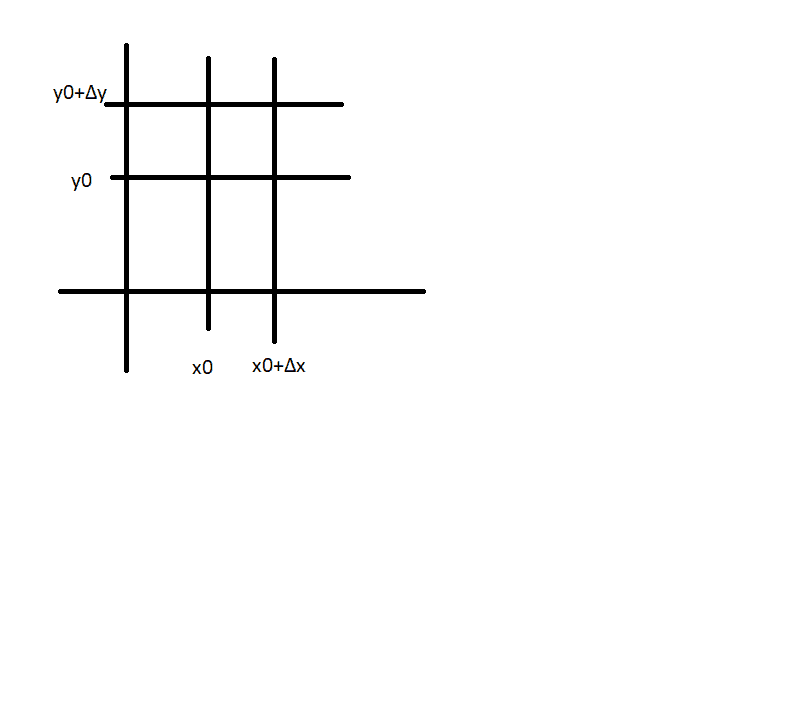
To generalise let u and v are both functions of x and y. By Holding y=y0 constant and changing x from x0 to x0+Δx this would result in changes in u and v.
Δu1≈ (∂u/∂x)Δx The partial derivatives evaluated at (x0,y0)
Δv1≈ (∂v/∂x)Δx
will serve as a good approximation to u and v at (x0+Δx,y0)
Similarly, holding x=x0+Δx and changing y from y0 to y0+Δy this will result in changes
Δu2≈ (∂u/∂y)Δy
Δv2≈ (∂v/∂y)Δy The partial derivatives evaluated at (x0+Δx,y0)
Holding y=y0+Δy and changing x from x+Δx to x0 will result in changes
Δu3≈ -(∂u/∂x)Δx
Δv3≈ -(∂v/∂x)Δx The partial derivatives evaluated at (x0+Δx,y0+Δy)
Holding x=x0 and changing y from y0+Δy to y0 will result in changes
Δu4≈ -(∂u/∂y)Δy
Δv4≈ -(∂v/∂y)Δy The partial derivatives evaluated at (x0,y0+Δy)
What I did was look at how u and v changed with each edge of the rectangle. But I cannot seem to get how the above fits together into forming the area in the uv system