kljoki
- 5
- 0
Hi
I have this graph
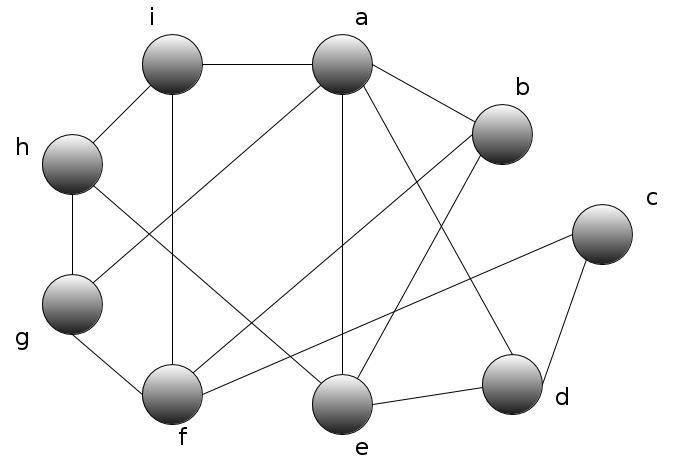
now i should check if this graph can be planar.
v - number of vertices
e - number of edges
f - number of faces
to be planar it should hold v - e + f = 2 from here f = 2 - v + e = 2 - 9 + 15 = 8
so f = 8 now my question is how to easily count faces (regions bounded by edges, including the outer, infinitely large region) of the graph??
thanks
I have this graph
now i should check if this graph can be planar.
v - number of vertices
e - number of edges
f - number of faces
to be planar it should hold v - e + f = 2 from here f = 2 - v + e = 2 - 9 + 15 = 8
so f = 8 now my question is how to easily count faces (regions bounded by edges, including the outer, infinitely large region) of the graph??
thanks