Circle normal to a vector

[DivergentSpectrum]

i have a 3d vector, and i want to draw a circle with a specified radius around the vector (for computer programming)
so i have the location of the center of the circle(first point of the vector)
but i also want the circle to be at a right angle to the vector

my approach:

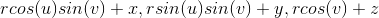
the equation of a sphere centered at x,y,z.
but i need to find the relation between u and v so that it forms a circle normal to some specified vector

please help thanks

 

[mfb]

That might be possible, but it looks complicated.

I would find two vectors u,v orthogonal to the specified vector (let's call it "n") and orthogonal to each other. This can be done with the cross-product. Afterwards you can combine them with sin and cos as in the 2-dimensional case.

 

[DivergentSpectrum]

if a plane normal to a vector x_n,y_n,z_n is given by

then i think i could replace the parametric sphere coordinates with the coordinates to the plane and solve

what i want out of this is the relation between u and v, but i can't figure out how to solve it
then once i have u and v in terms of a single t parameter i can center it at the correct point.

do you mean the u,v vectors as in the parameters? or something else?

 

[mfb]

do you mean the u,v vectors as in the parameters?

Probably a bad choice of variable names in my post. I mean two vectors.
I don't like the sphere approach. It might be possible, but I don't see the solution there while I am sure the other method works.

 

[HallsofIvy]

To "draw a circle normal to a vector" the first thing you need to do is find a plane normal to the vector. That's easy- if the plane is given by $$A\vec{i}+ B\vec{j}+ C\vec{k}$$ then any plane normal to it is of the form $$Ax+ By+ Cz= D$$ for some constant D. Finding D is another matter. A vector does not have a specified position in space.

 

[mfb]

The center of the circle seems to be given as (x,y,z).

 

[DivergentSpectrum]

i found this
http://demonstrations.wolfram.com/ParametricEquationOfACircleIn3D/
i don't know if i coded it wrong or what but its not working

 

[mfb]

We don't know either because you did not show what you did.

 

[DivergentSpectrum]

            double theta = Math.Atan2(curly[i, j, k], curlx[i, j, k]);
            double phi = Math.Acos(curlz[i, j, k] / Math.Sqrt(curlx[i, j, k] * curlx[i, j, k] + curly[i, j, k] * curly[i, j, k] + curlz[i, j, k] * curlz[i, j, k]));
            double costheta = Math.Cos(theta);
            double sintheta = Math.Sin(theta);
            double cosphi = Math.Cos(phi);
            double sinphi = Math.Sin(phi);

            int l = 0;
            double t ;
            int nitert = 20;
            double dt = 2 * Math.PI / nitert;
            double[] xcircle = new double[nitert+1];
            double[] ycircle = new double[nitert+1];
            double[] zcircle = new double[nitert+1];
            circlepoints.Add(new Point3D(-size * sinphi / 25 + xcurrent, size * cosphi / 25+ ycurrent, zcurrent));
        
  while (l <= nitert)
            {
                t = l * dt;
                xcircle[l] = -size * Math.Cos(t) * sinphi / 25 + size * Math.Sin(t) * costheta * cosphi / 25 + xcurrent;
                ycircle[l] = size * Math.Cos(t) * cosphi / 25 + size * Math.Sin(t) * costheta * sinphi / 25 + ycurrent;
                zcircle[l] = -size * Math.Sin(t) * sintheta / 25+ zcurrent;
                circlepoints.Add(new Point3D(xcircle[l], ycircle[l], zcircle[l]));
                circlepoints.Add(new Point3D(xcircle[l], ycircle[l], zcircle[l]));

                l++;
            }

I always feel bad asking people to look over my code lol.

anyway curlx,curly,curlz is the normal vector(yes I am doing a stokes theorem program :D)
and xcurrent,ycurrent,zcurrent is the position vector.

size/25 is the radius of the circle.

 

[ltkach2015]

Hey, don't know if I understand completely but here is what I think (btw I am still getting used to using the latex math symbols here so I won't use them in this response)

Use the cross product (copied&pasted this one):

Here the vector is normal to the circle's surface in the positive Z direction. That is the crossproduct of r's x component and y component.
Vector = rx cross ry

 

[ltkach2015]

Continuation of my last post:

syms u v
>>R = [u 0 0; 0 u*cos(v) 0; 0 0 u*sin(v)]

R =

[ u, 0, 0]
[ 0, u*cos(v), 0]
[ 0, 0, u*sin(v)]

>> vector = cross(R(1,: ),R(2,: ) )

vector =

[ 0, 0, u^2*cos(v)]

*had to edit away the simily faces

 

[DivergentSpectrum]

the wolfram site says:

While a 2D circle is parameterized by only three numbers (two for the center and one for the radius), in 3D six are needed. One set of parametric equations for the circle in 2D is given by

for a circle of radius

and center

.
In 3D, a parametric equation is

,
for a circle of radius

, center

, and normal vector

(

is the cross product). Here,

is any unit vector perpendicular to

. Since there are an infinite number of vectors perpendicular to

, using a parametrized

is helpful. If the orientation is specified by a zenith angle

and azimuth

, then

,

, and

can have simple forms:

,

,

.

but actually they made a mistake. here phi is the azimuth and theta is the zenith.
someone should probably tell them

 

[ltkach2015]

Hey,

example similar to: http://tutorial.math.lamar.edu/Classes/CalcIII/ParametricSurfaces.aspx

Afterwards, its the same process I went thru above with the cone