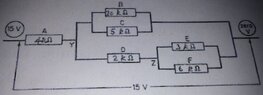
Circuit Diagram: Voltage & Current Calculation at Y & Z

  • Context: MHB 
  • Thread starter Thread starter Busybee12
  • Start date Start date
  • Tags Tags
    Circuits Diagram
Click For Summary
SUMMARY

The discussion focuses on calculating voltage at points Y and Z and the current through each resistor in a given circuit. Three primary methods are proposed for solving the problem: applying Kirchhoff's Voltage Law (KVL) using mesh currents, utilizing Kirchhoff's Current Law (KCL) at the nodes, and employing the equivalent resistance method. Each approach offers a systematic way to analyze the circuit, with KVL and KCL being particularly effective for complex circuits with multiple loops and nodes.

PREREQUISITES
  • Understanding of Kirchhoff's Voltage Law (KVL)
  • Familiarity with Kirchhoff's Current Law (KCL)
  • Knowledge of series and parallel resistor combinations
  • Basic circuit analysis techniques
NEXT STEPS
  • Study advanced applications of Kirchhoff's Voltage Law (KVL) in circuit analysis
  • Explore Kirchhoff's Current Law (KCL) for multi-node circuits
  • Learn about equivalent resistance calculations in complex circuits
  • Investigate mesh analysis techniques for circuit simplification
USEFUL FOR

Electrical engineering students, circuit designers, and anyone involved in circuit analysis and design will benefit from this discussion.

Busybee12
Messages
5
Reaction score
0
For the circuit shown below, determine
i) The voltage (V) at points Y and Z.
ii) The current through each resistor.

For (i) do I have to split into series and parallel?
 

Attachments

  • ScreenHunter_09 May. 22 14.55.jpg
    ScreenHunter_09 May. 22 14.55.jpg
    57 KB · Views: 90
Mathematics news on Phys.org
There are at least three approaches to solving this problem:

  1. Use KVL on the four mesh currents for each loop.
  2. Use KCL on each of the four nodes.
  3. Use the equivalent resistance method, and recursively work your way to the locations in which you're interested.

Which approach sounds the best to you?
 

Similar threads

Phasor diagrams for RLC circuit and resonant frequency
  • · Replies 3 ·
Replies
3
Views
4K
Understanding example in Wikipedia entry for open circuit voltage
  • · Replies 3 ·
Replies
3
Views
2K
Engineering Why is the voltage source high potential into node 1 at -12 V in this op amp problem?
  • · Replies 15 ·
Replies
15
Views
2K
MHB Solving Resistors in a Circuit: Working Backwards
  • · Replies 5 ·
Replies
5
Views
2K
Why Do Capacitors Behave Differently in Series and Parallel Configurations?
  • · Replies 20 ·
Replies
20
Views
2K
Phase difference RLC circuit
  • · Replies 5 ·
Replies
5
Views
3K
Engineering Analyzing the inductor current in the circuit
  • · Replies 1 ·
Replies
1
Views
1K
Current through an inductor as a function of time
  • · Replies 10 ·
Replies
10
Views
959
Calculation of current in driven series RLC circuit
  • · Replies 8 ·
Replies
8
Views
2K
Circuit calculation practice: voltage dividers, series, parallel
  • · Replies 1 ·
Replies
1
Views
4K