Circuit Problem -- Combining 4 resistors to make 95 Ohms

[a1234]

Homework Statement

1. Use resistors of 30 ohms, 40 ohms, 50 ohms, and 50 ohms to create a circuit with a total resistance of 95 ohms.

2. Find the amount of current going through two of these resistors if the circuit is attached to a source of 12 v.

3. What would be the voltage drops for the remaining two resistors?

2. The attempt at a solution

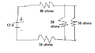
1) The diagram of the circuit is attached.

2) For the resistors of 50 ohms, the current running through them is I = V/R or I = 12/50 = 0.24 amps.

3) For the 30 ohm resistor, the drop is 12/70 * 30 = 360/70 volts.

For the 40 ohm resistor, the drop is 12/70 * 40 = 480/70 volts.

 

[BvU]

Hi a1,

What is your question ?
If you don't have one, I could ask: how exactly do you interpret part 2 of the exercise ? And 3 ? Does the exercise composer mean the circuit as found in part 1 or does he mean separate circuits -- if so, then what circuits ?

 

[scottdave]

There is Not 12 volts across the 50 ohm resistors. It is less than 12 volts. There is 12 volts across the entire circuit. Replace your parallel 50 ohm resistors with an 'equivalent 25 ohm' and try it then. Once you have the voltage across this 25 ohm 'resistor', go back and replace that with your parallel resistors to find the current through each.

 

[a1234]

There is Not 12 volts across the 50 ohm resistors. It is less than 12 volts. There is 12 volts across the entire circuit. Replace your parallel 50 ohm resistors with an 'equivalent 25 ohm' and try it then. Once you have the voltage across this 25 ohm 'resistor', go back and replace that with your parallel resistors to find the current through each.

If I use a 25 ohm resistor in place of the 50 ohm ones, is the circuit now considered to be in series completely? If that's the case, then the total resistance is 95 volts and the current across this 25 ohm resistor is 12/95 amps.
V = IR
V = 12/95 * 25 = 3.16 volts

For the current, is it I = 3.16/50 amps for each of the parallel resistors?

 

[scottdave]

Yes the 25 ohm equivalent resistor is in series with the rest of the circuit.

 

[a1234]

Is it correct that the current is 3.16/50 amps for each of the 50 ohm resistors? Are the values for the voltage drop of the other two resistors correct?

 

[haruspex]

Is it correct that the current is 3.16/50 amps for each of the 50 ohm resistors?

Yes.

Are the values for the voltage drop of the other two resistors correct?

No.
What is the current through each of them?

 

[scottdave]

At each node (intersection of components), the sum of currents entering the node must equal the sum of currents exiting the node. So the top of the two 50 ohm is a node. You know how much goes through each 50 ohm (exiting the node). Add those to find how much is entering the node. This is how much goes through the 40 ohm.

 

[a1234]

The total resistance is 95 ohms and the total voltage is 12 volts. The total current is 12/95 amps, and since this is a parallel connection the current is the same at both resistors. Then the voltage of the 40 ohm resistor is 12/95 * 40 = 480/95 volts. The voltage of the 30 ohm resistor is 12/95 * 30 = 360/95 volts.

 

[scottdave]

The total resistance is 95 ohms and the total voltage is 12 volts. The total current is 12/95 amps, and since this is a parallel connection the current is the same at both resistors. Then the voltage of the 40 ohm resistor is 12/95 * 40 = 480/95 volts. The voltage of the 30 ohm resistor is 12/95 * 30 = 360/95 volts.

All looks correct, except for the part about being parallel having the same current. Parallel branches have the same voltage, but not necessarily same current (only if each branch had same resistance). Series branches have the same current.

You may find the following videos useful.

 

[a1234]

That was a typo...I meant that since the 30 ohm and 40 ohm resistors are in series (not parallel), the current is the same at both places.

Thank you for all the help!