Solve Circuit: Find ΔQ for Switch T Turned Off

[hastings]

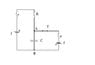
In the given circuit (1st diagram), the switch T is initially down (creates a connection). At a certain instant, the switch is turned off and for a while the circuit is kept in that state(final situation). Find the ΔQ=Q(fin)-Q(init) on the top plate of the capacitor while passing from the initial condition to the final condition. Please check out the diagrams. Consider all the quantities which appear in the diagrams, as known.


What I did:
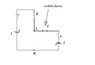
(1) When the switch is creating a connection, there is a current "I" which flows in the circuit BUT there is no current (or it tends to 0) in the piece of circuit containing the capacitor; we can consider it as an open switch or simply remove that piece (2nd diagram).
I need to know (Va-Vb) in order to determine the Q(int)

f-I(2r+R) +f =0

I=\frac{2f}{2r+R} (1.1)

(V_A-V_B) -Ir+f=0 \longrightarrow (V_A - V_B)=Ir-f (1.2)

Substituting (1.1) into (1.2), I get

(V_A - V_B)=\frac{2f}{2r+R}r-f

From that, I guess

Q^{init}=C(V_A-V_B)=C(\frac{2f}{2r+R}r-f)=C(-\frac{Rf}{2r+R}).

Is it correct up to this point?

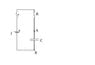
Now, how to proceed when the switch T is open and doesn't create connection (3rd diagram) with r and the 2nd source?

 

[hastings]

Let me try the second part. I'll refer to the 3rd diagram attached.
(2) I again need to know (Va-Vb) in order to find Q(fin). The current flows clock wise but I move counter clock wise because I have to go from A to B.

(V_A-V_B) +I(r+R) -f=0

(V_A-V_B)= f-I(r+R). (2.1)

In the above expression I substitute (1.1) and I get:

(V_A-V_B)= f-( \frac{2f}{2r+R} )(r+R) = \frac{2fr+fR-2fr-2fR}{2r+R}=-\frac{fR}{2r+R}

Q^{fin}=C(V_A-V_B)=C (-\frac{fR}{2r+R})

Hence

\Delta Q=Q^{fin}-Q^{init}= (- C\frac{fR}{2r+R}) -(-C\frac{Rf}{2r+R})

This cannot be possible!
Now, I clearly have mistaken somewhere! Plus, I think the current flowing in the circuit when switch T is off, is different from the current flowing when the switch is on, so I probably cannot use the same expression of "I", the current, in the 2nd part of the problem. Therefore, please help me!

 

[hastings]

Can anyone help me? thanks.