Discussion Overview
The discussion revolves around a homework problem involving capacitors in a circuit, specifically focusing on calculating the charge on capacitor C1 when certain switches are closed. Participants explore the concepts of equivalent capacitance, series and parallel configurations, and the application of the voltage divider equation.
Discussion Character
- Homework-related
- Technical explanation
- Conceptual clarification
Main Points Raised
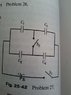
- One participant presents the problem with given values for capacitors and voltage, expressing confusion about the circuit configuration.
- Another participant questions whether the values provided represent capacitance in microfarads or charges in microcoulombs, emphasizing the importance of units.
- Clarification is provided that "C" refers to capacitors, and a link to a voltage divider equation is shared, although one participant admits to not being familiar with it.
- Participants discuss the calculations for equivalent capacitance, with one stating they found C12 = 3μF and C34 = 7μF for the parallel combinations, leading to an equivalent capacitance of Ceq = 2.1 μF when combined in series.
- There is a suggestion that the voltage across C1 can be determined using the voltage divider concept, which would then allow for the calculation of charge using the formula q = CV.
Areas of Agreement / Disagreement
Participants generally agree on the approach to solving the problem, but there is some uncertainty regarding the interpretation of the initial values (capacities vs. charges) and the application of the voltage divider equation.
Contextual Notes
There are unresolved assumptions regarding the definitions of the values given for the capacitors, and the participants have not fully established the correct application of the voltage divider equation in this context.