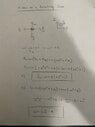Circular Motion: A coin on a rotating disk

[AzimD]

Homework Statement

A coin of mass m is on a rigid disk at a distance d from the center of the disk. There is
friction between the coin and the disk. The coefficient of static friction is µs. At time
t = 0, the disk begins to rotate with a constant angular acceleration of magnitude α.
The magnitude of the acceleration due to gravity is g.
Express your answers in terms of some or all of the given variables m, d, µs, α, t, and g
as needed.
(a) While the coin remains at rest relative to the disk, what is fs, the magnitude of
the force of static friction exerted by the disk on the coin as a function of time t?
(b) At what angular speed ω will the coin start to slip with respect to the disk?

Relevant Equations

F_c=md(ω^2)

I believe I've solved this problem, however, I got through it pretty quickly and since it's the last problem on the assignment, I feel that I may have had an oversight.
For part a, I got: fs=md(α^2)(t^2)
and for part b, I got: ω=Sqrt((µs*g)/d)

Could someone confirm my answers? I've attached a picture of the problem and my work!

 

[kuruman]

In part (a) you are correct that the net force on the coin is that of static friction. You are incorrect in assuming that the acceleration of the coin is only centripetal. You have to include the tangential component. That inclusion will, of course, affect the answer in part (b).

 

[AzimD]

In part (a) you are correct that the net force on the coin is that of static friction. You are incorrect in assuming that the acceleration of the coin is only centripetal. You have to include the tangential component. That inclusion will, of course, affect the answer in part (b).

Got it, I tried again, not sure if I got it right though. Could you check it? One other question that came up as I was doing the arithmetic is whether the a_r should be a negative quantity or not.

 

[kuruman]

Got it, I tried again, not sure if I got it right though.

It's not correct. $a_c$ and $a_r$ are acceleration components perpendicular to each other. You just don't add them as if they pointed in the same direction. Again, the net force on the coin is not centripetal, i.e. it does not point towards the center. Draw a free body diagram of the coin as seen from above.

One other question that came up as I was doing the arithmetic is whether the a_r should be a negative quantity or not.

Is the speed of the coin increasing or decreasing? That should answer your question.

 

[AzimD]

It's not correct. $a_c$ and $a_r$ are acceleration components perpendicular to each other. You just don't add them as if they pointed in the same direction. Again, the net force on the coin is not centripetal, i.e. it does not point towards the center. Draw a free body diagram of the coin as seen from above.

Is the speed of the coin increasing or decreasing? That should answer your question.

Got it, ya the issue regarding the acceleration components was an oversight by me. Rookie mistake.
Does this look right?

 

[erobz]

Got it, ya the issue regarding the acceleration components was an oversight by me. Rookie mistake.
Does this look right?

Part (a) looks ok.

For part (b) what component of the frictional force will it overcome to slip?

 

[kuruman]

For part (b) what component of the frictional force will it overcome to slip?

I am not sure I understand what you mean. The coin will not slip as long as $~F_{net}=m\sqrt{a_c^2+a_t^2}< \mu_s mg.$

 

[erobz]

I am not sure I understand what you mean. The coin will not slip as long as $~F_{net}=m\sqrt{a_c^2+a_t^2}< \mu_s mg.$

I'm probably confused. Isn't the tangential component of the frictional force fixed? To me it seems that only the radial component evolves in time. If it isn't slipping immediately in the tangential direction at $t= 0$ why would it at some future time $t$?

 

[kuruman]

The expression $f_s^{max}=\mu_sN$ does not specify the direction of the force. Yes, the tangential component is fixed. However, what is relevant here is the resultant of the tangential and centripetal accelerations. This resultant multiplied by the mass is the net force. Its expression as a function of time is, as OP eventually got, $$F_{net}=m~\alpha~ d\sqrt{1+\alpha^2t^4}.$$At $t=0$ the net force is tangential. As time increases, it tips towards the center and increases in magnitude. When the magnitude reaches $f_s^{max}$ the coin will start sliding in whatever direction the resultant acceleration points at that instant in time.

 

[haruspex]

I'm probably confused. Isn't the tangential component of the frictional force fixed? To me it seems that only the radial component evolves in time. If it isn't slipping immediately in the tangential direction at $t= 0$ why would it at some future time $t$?

It doesn’t slip independently in different directions. It either slips or it doesn’t. It doesn’t "know" about tangential versus radial.

 

[haruspex]

the coin will start sliding in whatever direction the resultant acceleration points at that instant in time

In that direction in the frame of the disk, that is. In the ground frame it's a little more complicated, think.

Edit: in the frame of the disk, in the opposite direction to that ground frame resultant.

 

[erobz]

The expression $f_s^{max}=\mu_sN$ does not specify the direction of the force. Yes, the tangential component is fixed. However, what is relevant here is the resultant of the tangential and centripetal accelerations. This resultant multiplied by the mass is the net force. Its expression as a function of time is, as OP eventually got, $$F_{net}=m~\alpha~ d\sqrt{1+\alpha^2t^4}.$$At $t=0$ the net force is tangential. As time increases, it tips towards the center and increases in magnitude. When the magnitude reaches $f_s^{max}$ the coin will start sliding in whatever direction the resultant acceleration points at that instant in time.

Ok, thanks for clarifying. I guess not everything is about resolving and analyzing in component directions. It doesn’t feel like I’ve ever ran into this before.

 

[jbriggs444]

In that direction in the frame of the disk, that is. In the ground frame it's a little more complicated, think.

It seems to me that the "direction of slip" would best be defined in terms of relative acceleration between mating surfaces at the point of contact and the instant of detachment^(*). That would, I think, be an invariant.

As long as we factor out the difference between the orientations of the two coordinate systems at the relevant instant, of course.

(*) The physical situation at the instant where static friction switches to kinetic friction may not be well modelled or amenable to differentiation. We might be better served by considering either the [invariant] direction of the force just prior to that instant. Or to the [invariant?] difference in accelerations just after.

 

[AzimD]

For part (b) what component of the frictional force will it overcome to slip?

I'm not sure if I understand your question, but if I do, then it would have to overcome µs.

 

[erobz]

I'm not sure if I understand your question, but if I do, then it would have to overcome µs.

Disregard my question, I got it wrong. Sorry if I caused you any confusion.

 

[AzimD]

Disregard my question, I got it wrong. Sorry if I caused you any confusion.

No worries! Does this mean that I got part b correct?

 

[haruspex]

No worries! Does this mean that I got part b correct?

Looks right to me.

 

[AzimD]

Thanks, guys! I once again appreciate the help! @kuruman @erobz @haruspex @jbriggs444

 

[haruspex]

It seems to me that the "direction of slip" would best be defined in terms of relative acceleration between mating surfaces at the point of contact and the instant of detachment

So, in the frame of the disc? But since it is initially at rest in that frame, that acceleration and the immediately ensuing velocity would be in the same direction.
However, I should have said that the slip direction in the disc's frame is opposite to its instantaneous acceleration in the ground frame.
The initial acceleration in the ground frame, after starting to slip, will be in the same direction as its prior acceleration, but diminished in magnitude.

There is one small flaw in the question: it overlooks the angular acceleration of the coin. That will require a frictional torque, leading to slippage occurring somewhat before the time calculated above. But that's a much more complicated matter.

 

[jbriggs444]

So, in the frame of the disc?

What I have in mind is not the coordinate acceleration of the coin as calculated in two different frames, but the difference in coordinate accelerations of coin and disc (so a "closing acceleration" if you will) in each of the two frames. It is my supposition (perhaps flawed) that this vector difference will have the same magnitude in any frame and also the same direction -- modulo the fact that the frames may not agree on the same zero direction at the time of first slip.

However, this is not germane to the subject matter of the thread and I was probably wrong to raise the distraction.