Circular Motion of a Cyclist and a Car going around a bend in the road

[AN630078]

Homework Statement

Hello, I have a question on the circular motion of the road but I am having a little difficulty answering it, specifically question 1 to find the radius from which other parts of the question lead on.

A cyclist is travelling on a bend in a road at 10ms^-1 and leans his bicycle at 20 degrees to the vertical in order to stay on the road. The total mass of the bicycle and cyclist is 90kg.

Question 1: What is the radius of the curvature of the bend of the road?

Question 2: On the same bend of the road a car of mass 1500kg travels at 25ms^-1. What frictional force would be required to keep the car’s tyres on the road?

Question 3: To eliminate the need for the frictional force on the cars tyres the road is banked, at what angle would this be?

I am very uncertain of my workings and wonder whether anyone may be of help, I would be very grateful for any guidance. I have attempted to solve the question as one can see but I do not know whether my approach would here be correct

Relevant Equations

centripetal acceleration=v^2/r
Centripetal force = mv^2/r
Force=mass*acceleration
θ=tan^-1(v^2/rg)

Question 1:

So we are given three variables;
Mass=90kg
Angle to the vertical = 20 degrees
Speed = 10 ms^-1
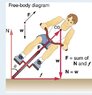
There is not enough information to rearrange the formulas for centripetal force or acceleration in terms of r to find the radius. However, I have a attached a free body diagram of a cyclist on a bend I found online.
The only external forces acting on the car are its weight w and the normal force of the road N, a frictionless surface can only exert a force perpendicular to the surface, a normal force. These two forces add to give a net external force that is horizontal toward the center of curvature and has magnitude mv2/r (the centripetal force). If the angle the cyclist leans θ is ideal for the speed and radius, then the net external force will equal the necessary centripetal force. Moreover, only the Normal force has a horizontal component which must be equal to the centripetal force; Nsinθ=mv^2/r.
The net vertical force must be zero, meaning that the vertical components of the two external forces must be equal in magnitude and opposite in direction. The vertical component of the normal force is N cos θ, and the other vertical force is the weight which must must be equal in magnitude; thus, N cos θ = mg.
Therefore, N=mg/cosθ
Substitute into the first equation;
mg(sinθ/cosθ)=mv^2/r
mg tan (θ)=mv^2/r
tan (θ)= v^2/rg
θ=tan^-1(v^2/rg)

(In hindsight I fear that in resolving the perpendicular component I have neglected the friction parallel to the road, which must supply the centripetal force. However, if the angle θ is ideal and at a certain speed there will not be a frictional force between the bicycle and the road. Is this formula correct or would it be wrong and not applicable here?)

However, if we rearrange this equation in terms of r;
r=v^2/g*tanθ
If I now input the known values to solve for r;

r=10^2/9.81*tan20
r=28.0069...~ 28.0 m to 3sf

Question 2;

As a car makes a turn, the force of friction acting upon the turned wheels of the car provides centripetal force required for circular motion.
F=mv^2/r
F=1500*25^2/28
F=33482.14286 ~ 33500 N to 3.s.f

Question 3:
Using the formula earlier derived;
θ=tan^-1(v^2/rg)
θ=tan^-1(25^2/28*9.81)
θ=66.27508...~ 66.3 degrees

 

[haruspex]

The only external forces acting on the car

Car?

its weight w and the normal force of the road N, a frictionless surface can only exert a force perpendicular to the surface, a normal force. These two forces add to give a net external force that is horizontal toward the center of curvature

The surface is not frictionless. Weight and normal force in this case add to zero since there is no vertical acceleration.

only the Normal force has a horizontal component

The road surface is horizontal. The normal force has no horizontal component.
But if you change all your mentions of normal force to be total reaction force (normal+friction) you arrive at, astonishingly

θ=tan^-1(v^2/rg)

the right answer.

 

[kuruman]

Perhaps a question for OP to ponder about is why does the cyclist have to lean into the turn anyway? The friction and normal force certainly don't disappear when he takes the turn upright, therefore the centripetal acceleration will still be there as will be the normal force necessary to support the weight. Anyone who has ridden a bicycle knows that it is a matter of "stability", but what is physically going on?

 

[AN630078]

Car?

The surface is not frictionless. Weight and normal force in this case add to zero since there is no vertical acceleration.

The road surface is horizontal. The normal force has no horizontal component.
But if you change all your mentions of normal force to be total reaction force (normal+friction) you arrive at, astonishingly

the right answer.

Thank you for your reply. Sorry I meant bicycle, I had muddled the vehicle of question 1 with question 2.
Oh, ok thank you for the clarification that the surface is not frictionless and that the normal force has no horizontal component.

Right so I have tried to correct my answer,
The external forces acting on the bicycle are its weight w and the normal force of the road N. There is no vertical acceleration since the resultant force is equal to zero. If the angle the cyclist leans θ is ideal for the speed and radius, then the net external force will equal the necessary centripetal force. Moreover, only the resultant force has a horizontal component which must be equal to the centripetal force; Nsinθ=mv^2/r.
The net vertical force must be zero, meaning that the vertical components of the two external forces must be equal in magnitude and opposite in direction. The vertical component of the Normal force is Ncos θ, and the other vertical force is the weight which must must be equal in magnitude; thus, N cos θ =mg.
Therefore, N=mg/cosθ
Substitute into the first equation;
mg(sinθ/cosθ)=mv^2/r
mg tan (θ)=mv^2/r
tan (θ)= v^2/rg
θ=tan^-1(v^2/rg)

r=v^2/g*tanθ
r=10^2/9.81*tan20
r=28.0069...~ 28.0 m to 3sf

So if this is indeed the correct answer for the radius, does that mean that my solutions to questions 2 and 3 would also be correct?

 

[kuruman]

The external forces acting on the bicycle are its weight w and the normal force of the road N.

Isn't friction also acting on the bicycle? Surely, the cyclist would not be able to execute the turn on very slippery ice. You need to rethink this. The normal force exerted by the horizontal road surface is along the vertical, opposite to the acceleration of gravity; it has no horizontal component to provide the centripetal acceleration.

When the surface is banked, as in Question 3, the normal force does have a horizontal component which makes it possible to eliminate friction.

 

[haruspex]

I have tried to correct my answer,

You do not seem to have understood what I wrote about normal force and total reaction force.
In this question, the road is horizontal, so the normal force is purely vertical. Nsin(θ) and Ncos(θ) do not come into it. But the reaction force from the road includes friction. Together, normal force and frictional force add up, as vectors, to form the total reaction force. Call this R. Rsin(θ) is the horizontal component (the frictional force) and Rcos(θ) is N.
Just change all the Nsin(θ) to Rsin(θ) and Ncos(θ) to Rcos(θ) in post #4 and it will be right.

 

[haruspex]

r=10^2/9.81*tan20

You should write that as 10^2/(9.81*tan20).

Question 2;
the force of friction acting upon the turned wheels

It acts on all four wheels.
The question could be worded better. The car's tyres will stay on the road, for a while at least, even if it skids. The frictional forces on different tyres will have different magnitudes and directions, so it should specify the total frictional force.
Your answer is correct.

Question 3:
Using the formula earlier derived;

Again, the right answer, but I have an awkward feeling that you just plugged the numbers into the formula without necessarily establishing that it applies in this way to this question. As @kuruman points out, it is a different scenario.