B Clarification on Length Contraction

[Ibix]

@NoahsArk - I said I'd draw Minkowski diagrams. Here's one in the rest frame of a rod that's ten light nanoseconds long (about ten feet):

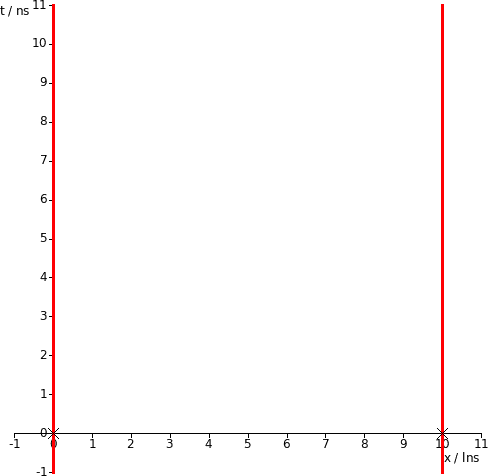
The two red lines represent the ends of the rod, not moving in this frame. I've also shown two crosses at time $t=0$, which represent a couple of firecrackers going off. Note that the rod is ten light nanoseconds long and the firecracker explosions are ten light nanoseconds apart.

Now here's the same thing in a frame where the rod is doing 0.6c.

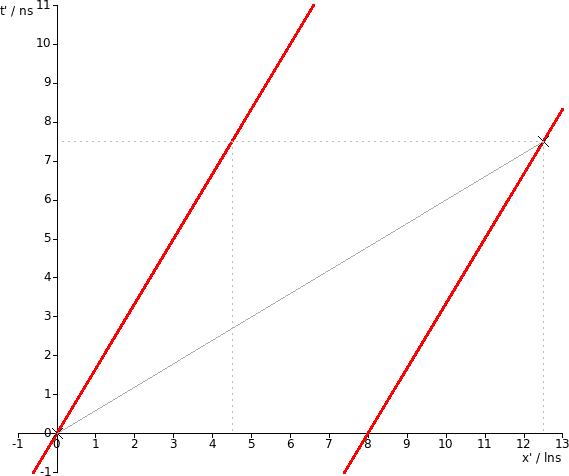
The two red lines again represent the front and back of the rod. The crosses represent the firecrackers, and there's a thin diagonal line joining them for clarity. I've also added various dotted lines connecting events to axes, again for clarity.

You can immediately see that the rod has length contracted by a factor of $\gamma=0.8$ - just read off the horizontal distance between the red lines. You can also see that the firecrackers are further apart by a factor of $1/\gamma=1.25$. And you can see that this isn't contradictory, it's just that the firecrackers went off at different times when the rod was in a different place, so the distance between them isn't the same as the length of the rod.

This is the mistake you make when you treat the Lorentz transforms as transforming distance: your process measured the distance between the flash at the front of the rod 7.5ns after the back passed the origin, and assumed that the back was at the origin.

 

[PeroK]

If you don't like Alice and Bob, use Pete and Ulysses.

Penelope and Ulysses would be better. Penelope representing the stay-at-home "stationary" frame of reference, and Ulysses representing the wandering "moving" frame.

The geometric aspect is interesting. When I first learned SR (six years ago now), it took about six weeks to really get the basics nailed down - it might have been a bit longer. To be honest, the only thing I didn't understand were spacetime diagrams. I remember being hopelessly lost about what the geometry of these things really was. So, I passed on that first time round. In general, I am much stronger algebraically than geometrically, which might have something to do with it.

That said, I learned recently that Einstein was slow to warm to Minkowski's hyperbolic geometry interpretation of SR. Maybe it isn't quite so natural as JL Synge believes. It's possible that he (and you) have very strong geometric visualisation skills that not everyone shares?

The real issue, of course, is how best to teach SR and, in this case, to help the OP understand length contraction. I'm not sure anyone really knows. And, indeed, it might be different for different students.

 

[phinds]

And here is another basic idea that I am not sure of which is likely making it confusing as well: When we say that the explosion happens at X distance from Alice, are we really saying that Alice could be standing anywhere in her coordinate system, but she observes the explosion to have happened X distance away from the origin? Or, does X = 10 mean 10 units from Alice and not ten units from what Alice has defined as her origin?

Why would "distance from Alice" mean anything other than "distance from Alice" ? What does anything else have to do with it?

 

[robphy]

I think there have been papers on the history of Minkowski’s hyperbolic trigonometry interpretation ( which has hyperbolic geometry only in the space of velocities) that relativity attracted more attention after Minkowski’s 1907/1908 paper. Maybe it was just the time to digest Einstein’s ideas from 1905... or maybe it was Minkowski validating these new ideas by Einstein.

When we describe general relativity in terms of the geometry of Spacetime, it was Minkowski that formulated it for flat space... using ideas from Felix Klein and Arthur Cayley. Minkowski gave us the “Spacetime” idea, as well “proper time” and “light cone”. After initial resistance by Einstein, he embraced the idea and generalized the geometry to a curved one.

Byrecognizing Minkowski spacetime geometry, one can pull in one’s vast knowledge of Euclidean geometric thinking, suitably tweaked to handle the signature. Otherwise, one is just doing algebra with \gamma’s and v\gamma not realizing those are essentially cosines and sines, interpreted as ratios of sides of a right triangle. Just like algebra can be a crutch for physical understanding, geometry can as well.
(We tell students to draw position vs time graphs, free body diagrams, ray tracing diagrams, why not fancier position vs time graphs: Spacetime diagrams?)

(Without a Spacetime diagram and it’s geometry, how would one explain “light cone” if one only drew boxcars in relative motion? Or, later, explain the bending of light by the sun? Or the behavior near the event horizon of a black hole?)

 

[Ibix]

That said, I learned recently that Einstein was slow to warm to Minkowski's hyperbolic geometry interpretation of SR. Maybe it isn't quite so natural as JL Synge believes. It's possible that he (and you) have very strong geometric visualisation skills that not everyone shares?

I certainly learned the algebra first, but the realisation that you could just mentally sketch a displacement-time diagram and then sketch a boost by sliding events along hyperbolae was great for understanding it. Partly because it's impossible to forget the relativity of simultaneity like this...

 

[robphy]

I think spacetime diagrams are considered hard or too mathematical because
that was Einstein's first impression of them, and
many introductory physics textbooks take a historical/pseudo-historical development of relativity
[focusing on the ether, michelson morley, Einstein 1905, and then the classic effects (what I sometimes consider the classic traps and pitfalls) , and then appeal to experimental verification]
but very little on the more modern spacetime view of (that mathematician) Minkowski,
which might help develop intuition.

It's refreshing to see a new intro textbook (maybe not so new anymore) like Tom Moore's
Six Ideas that Shaped Physics, Unit R. http://www.physics.pomona.edu/sixideas/

(I like to point out that
the position-vs-time graphs of PHY 101
has an underlying non-euclidean geometry:
the Galilean geometry.
If you draw the clock effect/twin paradox scenario in Galilean physics, you get a triangle
where the kinked worldline of the traveler has the same length
(where arc-length is proper-time, measured with a wristwatch carried by that observer)
as the stay at home twin. That is, no time difference along the paths,
However, that triangle doesn't satisfy the triangle inequality.
In addition,
a t=const line is [Galilean-]perpendicular to all worldlines, regardless of their velocities (slopes)... which is the condition of "absolute time" and "absolute simultaneity".
That doesn't sound Euclidean.
However, we have been taught to read that ordinary position-vs-time graph a certain way.
So, we are generally unaware of it to complain about its nonEuclidean features
...but enter the spacetime diagram for special relativity... )

(Last quote, then I'll get off my soapbox.

http://aapt.scitation.org/doi/10.1119/1.17728
"Lapses in Relativistic Pedagogy" by Mermin
makes some good points

...Lorentz transformation doesn't belong in a first exposure to special relativity. Indispensable as it is later on, its very conciseness and power serve to obscure the subtle interconnnectedness of spatial and temporal measurements that makes the whole business work. Only a loonie would start with real orthogonal matrices to explain rotations to somebody who had never heard of them before, but that's how we often teach relativity. You learn from the beginning how to operate machinery that gives you the right answer but you acquire little insight into what you're doing with it.

)

Now... back to the ideas for this thread.
As others have said, and as some of us have done,
draw a spacetime diagram.

(Since you don't usually solve a geometry problem with rotation matrices,
it might be good to try to solve special relativity problems using methods other than just the formulas for Lorentz transformations, length-contraction, or time-dilation.
Try trigonometry.)

 

[PeroK]

(Since you don't usually solve a geometry problem with rotation matrices,
it might be good to try to solve special relativity problems using methods other than just the formulas for Lorentz transformations, length-contraction, or time-dilation.
Try trigonometry.)

In other words, rely on the student's intuitive understanding of hyperbolic trigonometry.

 

[robphy]

In other words, rely on the student's intuitive understanding of hyperbolic trigonometry.

Um... no...

develop the understanding of hyperbolic trigonometry using circular trigonometry, which they probably developed by drawing free body diagrams and breaking vectors into components. Why not use what they know and build on it (even though it wasn’t Einstein’s method of calculation or intuition)?

[From asking folks at the Einstein Papers project if Einstein reasoned with Spacetime diagrams, no one could point to an example that wasn’t a simple sketch, and such sketches didn’t solve a problem].I think that’s better than using transformation equations expressed in terms of slopes... (we don’t even teach rotations with slopes!) at least use the analogue of the angle (scary word: rapidity).

Let me just say that as a physics professor whose been a regular at AAPT meetings, I’ve spoken to all sorts of teachers and students who struggle with relativity. Since the standard way doesn’t seem to help, I’m looking for alternative ways to teach relativity.
Some of these methods have been in the literature but are obscure or forgotten or not developed enough. I visit here at PF and at PSE to look for problems (some simple and some more challenging) that could be clarified and solved with a Spacetime diagram... using my diamonds or my Spacetime trig methods...
in some sense, I’m doing research.

 

[NoahsArk]

PeroK: You cleared up some misconceptions I was having! Getting some rest over the weekend is letting me see things more clearly:) The fact that the position of the observers doesn't matter takes away a lot of confusion. Although using human names in the problem still can be a helpful crutch, I think, I see that it's necessary to know, when doing so, that what really matters is what's happening in the primed and unprimed frames, S and $S ^\prime$, and that when we say something happened at x, it doesn't mean that something happened x units away from an observer like Alice, it means that something happened x units away from the origin of the observer's frame: the S origin.

That still leaves an important question, and I think I answered the question for myself today: Should we assume, when doing Lorentz transformations, that the origins of the S and $S ^\prime$ frames are aligned at the reference event? I think the answer must be yes, and the same is true for Galilean transformations? If that's true, I didn't need, in my example, to say that Alice and Bob were aligned at (0,0). The origins of their S and $S ^\prime$ frames were aligned at some reference event, and it doesn't really matter what the reference event was.

Ibix: thank you for the space-time diagram. Can we illustrate both frame's perspective on a single diagram, and is that a good idea to do? I will follow up with some additional questions on the diagram you posted.

PeterDonis: you told me to try and draw a space time diagram which I have done. It was helpful, but you will see I ran into a problem:

The explosion (marked with a circle) happened in the S frame at (0, 10) (side note- the left number when I indicate a pair of coordinates should be t, and the right number should be x, right?). In the $S ^\prime$ frame, the event happened at (-7.5, 12.5). The red line here is the world line of the $S ^\prime$ frame. The dotted line is the $S ^\prime$ frame's line of simultaneity at the moment the explosion happened. The first thing I want to confirm is that on this diagram I should only be drawing one circle for the explosion, and I should not be drawing two circles - one for where it happened in each frame?

What I am not sure how to do is how to illustrate that the explosion happened at x = 12.5 in the $S ^\prime$ frame without drawing a new diagram? Another problem you see in this picture is that when you draw the line of simultaneity with the right slope (which is .6 as Pencilvester showed in another thread), the line of simultaneity intercepts the time axis at the wrong time. Rather than intersecting at -7.5, it intersects at around - 6. The only reason why I can think of of this happening is because the gaps between the lines of simultaneity in the $S ^\prime$ frame are smaller than they are in the S frame, and therefore you can draw 7.5 of them from the origin until the point where the line of simultaneity of the explosion intercepts with the t axis?

 

[Pencilvester]

the line of simultaneity intercepts the time axis at the wrong time. Rather than intersecting at -7.5, it intersects at around - 6.

A time axis can be thought of as the worldline of the spacial origin for a specific frame, i.e. the line given by equation $x=0$. There is a unique one for each frame. The worldline of the S’ spatial origin is the red line you drew. That is the time axis for S’. But because Euclidean geometry isn’t applicable to spacetime diagrams, you could measure the distance of the point of intersection with that line to the origin in a naively Euclidean manner, and it still won’t be 7.5. You’d have to use the Minkowski metric to get the correct “distance” ($ds^2 = -dt^2 + dx^2$).

 

[PeroK]

PeroK: You cleared up some misconceptions I was having! Getting some rest over the weekend is letting me see things more clearly:) The fact that the position of the observers doesn't matter takes away a lot of confusion. Although using human names in the problem still can be a helpful crutch, I think, I see that it's necessary to know, when doing so, that what really matters is what's happening in the primed and unprimed frames, S and $S ^\prime$, and that when we say something happened at x, it doesn't mean that something happened x units away from an observer like Alice, it means that something happened x units away from the origin of the observer's frame: the S origin.

Yes!

That still leaves an important question, and I think I answered the question for myself today: Should we assume, when doing Lorentz transformations, that the origins of the S and $S ^\prime$ frames are aligned at the reference event? I think the answer must be yes, and the same is true for Galilean transformations? If that's true, I didn't need, in my example, to say that Alice and Bob were aligned at (0,0). The origins of their S and $S ^\prime$ frames were aligned at some reference event, and it doesn't really matter what the reference event was.

The often unstated rule is that to use the Lorentz Transformation the origins (which means $x= 0, t=0$ and $x'=0, t'=0$) must coincide. That's the reference event.

 

[jbriggs444]

Why would "distance from Alice" mean anything other than "distance from Alice" ? What does anything else have to do with it?

Distance from where Alice is, distance from where Alice was or distance from where Alice will be? Presumably the intent is "distance from here to where Alice is at this moment". Using coordinates makes it somewhat more obvious that a choice of simultaneity convention may become important.

 

[NoahsArk]

@Ibix the diagram helps me understand the difference between length contraction and the Lorentz transformation for x. If a rod, 10 light nanoseconds long, is in a rocket flying with it, then the rod is stationary with respect to the rocket observer. I am assuming that is what your first diagram represents? (It still helps me to visualize by using terms like "rocket observer", but I'm doing so now keeping in mind the clarifications that have been made above.) Your second diagram could be the from the frame of reference of someone on Earth watching the rocket go by correct?

I've also shown two crosses at time t=0, which represent a couple of firecrackers going off.

So, does this mean that according to the rocket observer, two fire crackers are going off at the same time, one on each end of the rod? For the rocket observer, one fire cracker goes off at x = 10 and the other at x = 0 which is where the ends of the rods are sitting in the rocket frame? If this is the case, it makes more sense that for the Earth observer, because of the leading clocks lag rule, the explosion at the front of the ship would happen after it happened for the rocket observer. As we've been discussing, it happened 7.5 seconds later according to the Earth observer. When I look at your second diagram, I see that the front of the rod begins at x = 8 in the Earth frame, and ends up at x = 12.5. That makes sense because it took 7.5 seconds of travel time in the Earth frame, and 7.5 x .6v = 4.5 nanoseconds of distance that it traveled to get from x = 8 to x = 12.5. Have I worked out what's going on correctly? I assume the back of the rod starts out at 0,0 in both frames?

@robphy I agree that visualizing things is helpful. In my case, it helped me a lot to understand the term $\gamma vX ^\prime$ as the leading clocks lag rule by seeing v as the slope of the line and realizing that the bigger $x ^\prime$ is, the higher on the time access you will go due to the fact that $x ^\prime$ is slopping upward.. Some of your comments regarding light cones and using right triangles as visual aides gave me some food for thought. Some of the concepts you brought up though, while interesting, are advanced for me at this point, and I will need time to be able to get the background. Once the examples go beyond the use of basic algebra and geometry as tools, I would need to learn the higher level math to be able to follow (which I intend to do in the future, but am not there yet).

Thank you.

 

[Ibix]

I am assuming that is what your first diagram represents? (It still helps me to visualize by using terms like "rocket observer", but I'm doing so now keeping in mind the clarifications that have been made above.) Your second diagram could be the from the frame of reference of someone on Earth watching the rocket go by correct?

Yes.

So, does this mean that according to the rocket observer, two fire crackers are going off at the same time, one on each end of the rod? For the rocket observer, one fire cracker goes off at x = 10 and the other at x = 0 which is where the ends of the rods are sitting in the rocket frame? If this is the case, it makes more sense that for the Earth observer, because of the leading clocks lag rule, the explosion at the front of the ship would happen after it happened for the rocket observer. As we've been discussing, it happened 7.5 seconds later according to the Earth observer. When I look at your second diagram, I see that the front of the rod begins at x = 8 in the Earth frame, and ends up at x = 12.5. That makes sense because it took 7.5 seconds of travel time in the Earth frame, and 7.5 x .6v = 4.5 nanoseconds of distance that it traveled to get from x = 8 to x = 12.5. Have I worked out what's going on correctly? I assume the back of the rod starts out at 0,0 in both frames?

Yes, assuming you meant 7.5 × 0.6$c$ and the v was a typo.

 

[NoahsArk]

To try and further understand what's happening, I thought about it and made this diagram:

The bottom is the rocket, $x ^\prime$ coordinate system. The top is the earth, x, coordinate system- say it's a road. At each place where a number is drawn on the Earth system there is a post on the road. In the rocket, which is flying next to the road, one person stands at $x ^\prime = 0$ and the other at $x ^\prime = 10$. Instead of firecrackers going off at those points, as in the previous example, each person, simultaneously in the rocket frame, waves a paint brush out of the window and puts paint on Earth observer's posts. The event representing the second paintbrush being waved at $x ^\prime = 10$ in the rocket frame, similar to the firecracker example, will be seen as happening at x = 12.5 in the Earth frame.

I think the above diagram, correct me if I'm wrong, illustrates another point: As we discussed, the Earth observer will explain why this event happened at 12.5 in their frame as being due to the relativity of simultaneity- i.e. the second paint brush wasn't waved until a later time and therefore it had to travel further down the road before making it's mark. However, the rocket observer won't say that ROS is the reason for the second paint brush getting paint on post number 12.5. They will say that Earth's posts have been cramped together by a factor of .8, and that's why the person standing 10 units from the origin of the rocket frame was able to reach out to a post 12.5 units from the origin in the Earth frame. Does this describe things correctly from the rocket perspective?

 

[PeterDonis]

The bottom is the rocket, $x ^\prime$ coordinate system. The top is the earth, $x$, coordinate system

No, they aren't, because you've left out time. You need to draw a spacetime diagram. Just space alone is wrong.

 

[PeterDonis]

The first thing I want to confirm is that on this diagram I should only be drawing one circle for the explosion

That's correct. The explosion is one event. That means it is one point in spacetime, so it's one point on the diagram.

What I am not sure how to do is how to illustrate that the explosion happened at x = 12.5 in the $S^\prime$ frame

That is the spacetime interval between the explosion event and the event where your $x^\prime = - 7.5$ line of simultaneity (the dotted line) crosses the worldline of the $S^\prime$ origin (the red line). So you should find that

$$
\sqrt{\left( \Delta x \right)^2 - \left( \Delta t \right)^2} = 12.5
$$

where $\Delta x$ is the difference in $x$ coordinates between the two events, and $\Delta t$ is the difference in $t$ coordinates between the two events. We know the explosion is at $t = 0$, $x = 10$. The other event, as you can calculate from the inverse Lorentz transform and the fact that in the primed frame its coordinates are $t^\prime = - 7.5$, $x^\prime = 0$, will have coordinates $t = - 9.375$,. $x = - 15.625$. So we have $\Delta x = 21.25$ and $\Delta t = 18.25$, and thus

$$
\sqrt{\left( \Delta x \right)^2 - \left( \Delta t \right)^2} = = \sqrt{15.625^2 - 9.375^2} = 12.5
$$

 

[NoahsArk]

No, they aren't, because you've left out time. You need to draw a spacetime diagram. Just space alone is wrong.

What I meant to say is, these are their x axis. In the question I am only trying to understand what is happening to their respective x coordinates, and not what's happening to their t coordinates.

 

[PeterDonis]

In the question I am only trying to understand what is happening to their respective x coordinates, and not what's happening to their t coordinates.

And what we are all trying to tell you is that you can't do that, because what happens to their x coordinates and what happens to their t coordinates are connected. You simply can't look at them separately. If you keep trying to all you are going to do is continue to get wrong answers and have problems understanding what's going on and frustrate all of us who are trying to help you.

 

[robphy]

To try and further understand what's happening, I thought about it and made this diagram:
[snip]

While the diagram is correct only if appropriately interpreted, it is limited.

A spacetime diagram below suggest the following interpretation:
It describes how the Earth frame
compares its x-axis tickmarks with the rocket frame's x'-axis tickmarks.
The correspondence follows the Earth frame lines.
Is that how you interpret it?By the principle of relativity, there is a similar diagram with the Earth's x-axis at the bottom and the rocket x-axis at the top... and it will be description of how the rocket frame compares...

But your diagram, as is... with the bottom axis as the rocket frame and the top axis as the Earth frame, can't be used to explain this.

As @PeterDonis says, you really need a spacetime diagram.

Based on my spacetime diagram back in post #11,
you can make a comparison of x-axes by extending lines
parallel to the worldlines (and the timelike diagonal of the diamonds).

In fact, every calculation that you might want to make about this situtation
can be read off by doing some counting on this diagram.

 

[NoahsArk]

I appreciate all the help.

A spacetime diagram below suggest the following interpretation:
It describes how the Earth frame
compares its x-axis tickmarks with the rocket frame's x'-axis tickmarks.
The correspondence follows the Earth frame lines.
Is that how you interpret it?

Yes. The blue rectangles are the rocket's space units and the red diamonds are Earth's space units right?

That is the spacetime interval between the explosion event and the event where your x′=−7.5x′=−7.5x′ = - 7.5 line of simultaneity (the dotted line) crosses the worldline of the S′ origin (the red line). So you should find that √(Δx)2−(Δt)2=12.5

I will have to give that some thought. This looks like the invariant interval in reverse. I remember reading that you use this instead when you have two events that are separated by space by not by time in a certain frame. The invariant interval for time gives us proper time, so does this version of the invariant inverval give proper distance?

Sorry my latex botches things in quotes.

 

[PAllen]

I will have to give that some thought. This looks like the invariant interval in reverse. I remember reading that you use this instead when you have two events that are separated by space by not by time in a certain frame. The invariant interval for time gives us proper time, so does this version of the invariant inverval give proper distance?

Sorry my latex botches things in quotes.

Yes, the invariant interval for spacelike separated events is proper distance i.e. distance in a frame where the events are simultaneous.

 

[robphy]

The blue rectangles are the rocket's space units and the red diamonds are Earth's space units right?

Yes, the red diamonds are for the earth/lab frame.
The blue diamonds are for the rocket frame.

"diamonds" or "parallelograms" [or "boxes"] are accurate descriptions.

However, "rectangles" or "squares" are not...
because (despite Euclidean appearances), the edges are not "Minkowski-perpendicular" to each other.
More generally, one set of lightlike lines (the 45-degree lines) are not "Minkowski-perpendicular" to the other set of lightlike lines (at minus-45-degrees). Their Minkowski-dot-product is not zero.
The diagonals, however, are Minkowski-perpendicular.
(A lot of the geometry of Minkowski spacetime is encoded in those diamonds.)