- #1
Ziks
- 6
- 0
Firstly, I apologise if this is the wrong section, but as far as I could tell this was the most relevant.
I have a pair of triplets [itex](p1, y1, r1)[/itex] and [itex](p2, y2, r2)[/itex]. Each one describes a set of roll, yaw, and pitch rotations in that order, by the angles given by each component in respective order. In my scenario, pitch is a rotation about the Y axis, yaw about Z, and therefore roll about X. Also, the angles are in degrees for my application.
My overall aim is to produce a third triplet [itex](p3, y3, r3)[/itex] that describes the combined transformation of the first triplet and the second, in that order.
My initial naive solution was to simply add each component like so:
[itex](p3, y3, r3) = (p1 + p2, y1 + y2, r1 + r2)[/itex]
This works for some very simple inputs, such as when all the components of the first or second rotation are all 0, or both rotations are 0 on all but the same axis. My second approach was to convert both rotations to matrices, multiply the matrices, and then extract the new pitch, yaw and roll angles from that. This is my working, although I may have made an error:
[itex]
\begin{array}{rl}
pitch(p) &= \begin{bmatrix}
cos(p) & 0 & sin(p) \\
0 & 1 & 0 \\
-sin(p) & 0 & cos(p) \end{bmatrix} \\ \\
yaw(y) &= \begin{bmatrix}
cos(y) & -sin(y) & 0 \\
sin(y) & cos(y) & 0 \\
0 & 0 & 1 \end{bmatrix} \\ \\
roll(r) &= \begin{bmatrix}
1 & 0 & 0 \\
0 & cos(y) & -sin(y) \\
0 & sin(y) & cos(y) \end{bmatrix}
\end{array}
[/itex]
To find the composite transformation [itex]T[/itex] from a given [itex](p, y, r)[/itex] triplet:
[itex]
T = pitch(p) \times yaw(y) \times roll(r) = \begin{bmatrix}
\color{blue}{cos(p)cos(y)} & -cos(p)sin(y)cos(r) + sin(p)sin(r) & cos(p)sin(y)sin(r) + sin(p)cos(r) \\
\color{green}{sin(y)} & \color{red}{cos(y)cos(r)} & \color{red}{-cos(y)sin(r)} \\
\color{blue}{-sin(p)cos(y)} & sin(p)sin(y)cos(r) + cos(p)sin(r) & -sin(p)sin(y)sin(r) + cos(p)cos(r)\end{bmatrix}
[/itex]
Now I want to extract a [itex](p, y, r)[/itex] triplet from a given transformation [itex]T[/itex]:
[itex]
(p, y, r) = (atan2(-\color{blue}{T_{31}}, \color{blue}{T_{11}}), arcsin(\color{green}{T_{21}}), atan2(-\color{red}{T_{23}}, \color{red}{T_{22}}))
[/itex]
Where [itex]atan2[/itex] is defined as (from wikipedia):
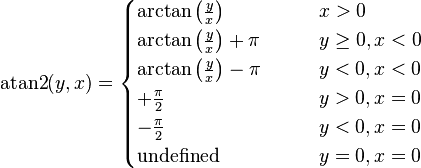
This only works for inputs where [itex]-90 \lt y \lt 90[/itex], because [itex]sin(y) = sin(180-y)[/itex] and so [itex]arcsin(sin(y)) \ne y[/itex] when [itex]y \lt -90[/itex] or [itex]90 \lt y[/itex]. Let's try a simple example input where this fails:
[itex]
T = pitch(0) \times yaw(135) \times roll(0)
[/itex]
[itex]
(p, y, r) = (atan2(-T_{31}, T_{11}), arcsin(T_{21}), atan2(-T_{23}, T_{22})) = (180, 45, 180)
[/itex]
This is almost a valid answer, because [itex](180, -45, 180)[/itex] is the same transformation as [itex](0, 135, 0)[/itex].
Is there a simpler way of combining two pitch, yaw, roll transformations? If not, is there a nice way of preserving the sign of [itex]y[/itex] and fixing my method?
I am by no means a mathematician or physicist, but I've made an attempt using what little trigonometry and linear algebra I know. Despite the apparent simplicity of the problem, I couldn't find anything using Google.
Thank you in advance.
I have a pair of triplets [itex](p1, y1, r1)[/itex] and [itex](p2, y2, r2)[/itex]. Each one describes a set of roll, yaw, and pitch rotations in that order, by the angles given by each component in respective order. In my scenario, pitch is a rotation about the Y axis, yaw about Z, and therefore roll about X. Also, the angles are in degrees for my application.
My overall aim is to produce a third triplet [itex](p3, y3, r3)[/itex] that describes the combined transformation of the first triplet and the second, in that order.
My initial naive solution was to simply add each component like so:
[itex](p3, y3, r3) = (p1 + p2, y1 + y2, r1 + r2)[/itex]
This works for some very simple inputs, such as when all the components of the first or second rotation are all 0, or both rotations are 0 on all but the same axis. My second approach was to convert both rotations to matrices, multiply the matrices, and then extract the new pitch, yaw and roll angles from that. This is my working, although I may have made an error:
[itex]
\begin{array}{rl}
pitch(p) &= \begin{bmatrix}
cos(p) & 0 & sin(p) \\
0 & 1 & 0 \\
-sin(p) & 0 & cos(p) \end{bmatrix} \\ \\
yaw(y) &= \begin{bmatrix}
cos(y) & -sin(y) & 0 \\
sin(y) & cos(y) & 0 \\
0 & 0 & 1 \end{bmatrix} \\ \\
roll(r) &= \begin{bmatrix}
1 & 0 & 0 \\
0 & cos(y) & -sin(y) \\
0 & sin(y) & cos(y) \end{bmatrix}
\end{array}
[/itex]
To find the composite transformation [itex]T[/itex] from a given [itex](p, y, r)[/itex] triplet:
[itex]
T = pitch(p) \times yaw(y) \times roll(r) = \begin{bmatrix}
\color{blue}{cos(p)cos(y)} & -cos(p)sin(y)cos(r) + sin(p)sin(r) & cos(p)sin(y)sin(r) + sin(p)cos(r) \\
\color{green}{sin(y)} & \color{red}{cos(y)cos(r)} & \color{red}{-cos(y)sin(r)} \\
\color{blue}{-sin(p)cos(y)} & sin(p)sin(y)cos(r) + cos(p)sin(r) & -sin(p)sin(y)sin(r) + cos(p)cos(r)\end{bmatrix}
[/itex]
Now I want to extract a [itex](p, y, r)[/itex] triplet from a given transformation [itex]T[/itex]:
[itex]
(p, y, r) = (atan2(-\color{blue}{T_{31}}, \color{blue}{T_{11}}), arcsin(\color{green}{T_{21}}), atan2(-\color{red}{T_{23}}, \color{red}{T_{22}}))
[/itex]
Where [itex]atan2[/itex] is defined as (from wikipedia):
This only works for inputs where [itex]-90 \lt y \lt 90[/itex], because [itex]sin(y) = sin(180-y)[/itex] and so [itex]arcsin(sin(y)) \ne y[/itex] when [itex]y \lt -90[/itex] or [itex]90 \lt y[/itex]. Let's try a simple example input where this fails:
[itex]
T = pitch(0) \times yaw(135) \times roll(0)
[/itex]
[itex]
(p, y, r) = (atan2(-T_{31}, T_{11}), arcsin(T_{21}), atan2(-T_{23}, T_{22})) = (180, 45, 180)
[/itex]
This is almost a valid answer, because [itex](180, -45, 180)[/itex] is the same transformation as [itex](0, 135, 0)[/itex].
Is there a simpler way of combining two pitch, yaw, roll transformations? If not, is there a nice way of preserving the sign of [itex]y[/itex] and fixing my method?
I am by no means a mathematician or physicist, but I've made an attempt using what little trigonometry and linear algebra I know. Despite the apparent simplicity of the problem, I couldn't find anything using Google.
Thank you in advance.
Last edited: