Comparing angular momentum/energy of orbits

[conquerer7]

Homework Statement

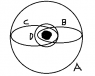
Attached. A and D are circular. Find the orbit with largest angular momentum, largest total energy, and largest maximum speed.

Homework Equations

E is proportional to -1/a (elliptical; a is semimajor axis)
U is proportional to -1/r
K is proportional to 1/r (circular only)
dA/dt is proportional to L
T^2 is proportional to a^3

The Attempt at a Solution

I want to see somebody work it out the 'right' way, since I'm more or less fooling around with no idea what I'm doing.

(a) I have (not sure) that L is proportional to sqrt(r) for circular orbits, so A is higher than D. Since C and B are going slower than A at aphelion, A beats them too. So the answer is A?
(b) is A since it has the largest semimajor axis.
(c) No idea; I know it's not D, but then I'm not sure on the rest. A has highest energy, B has much less but makes a much closer approach.

 

[dynamicsolo]

Your answer to (b) is correct: the total mechanical energy of bound orbits is negative, so larger total energies are "less negative".

For (c), they are asking which orbit has some point at which the speed is greater than for any point on any of the other orbits. Larger speed means larger kinetic energy K. What determines the speed of an object at some point on its orbit?

On (a), I don't know how much they've discussed with you in your course concerning elliptical orbits. You want to consider Kepler's Second Law and the way in which a line from the central body to orbiting object (say, star to planet) "sweeps out" area in a set time interval. Where along the orbit would the largest-area "wedge" be swept out in a day? Which orbit would produce a larger wedge than any of the others? Keep in mind that speeds along orbits are disproportionately faster with closer distance to the central body. (This question is trickier than the other two.)

 

[gneill]

A relationship that may help you decide the answer for part (c) is, for any orbit:

v(r,a) = \sqrt{\mu \left(\frac{2}{r} - \frac{1}{a} \right)}

Now, \mu is the same for all of the orbits under consideration since they're all orbiting the same central body. So for comparison purposes you can set it to unity and there will be no loss of generality for this problem.

If you add a crude scale to the given diagram you should be able to find estimates of r and a for each orbit at perihelion. (For circular orbits r = a).