Complementary Angles: A Visual Explanation

[mcastillo356]

Homework Statement

Useful identities
Many important properties of $\cos t$ and $\sin t$ are deduced from the fact they are the coordinates of the point $P_t$ in the circunference $C$, with equation $x^2+y^2=1$.
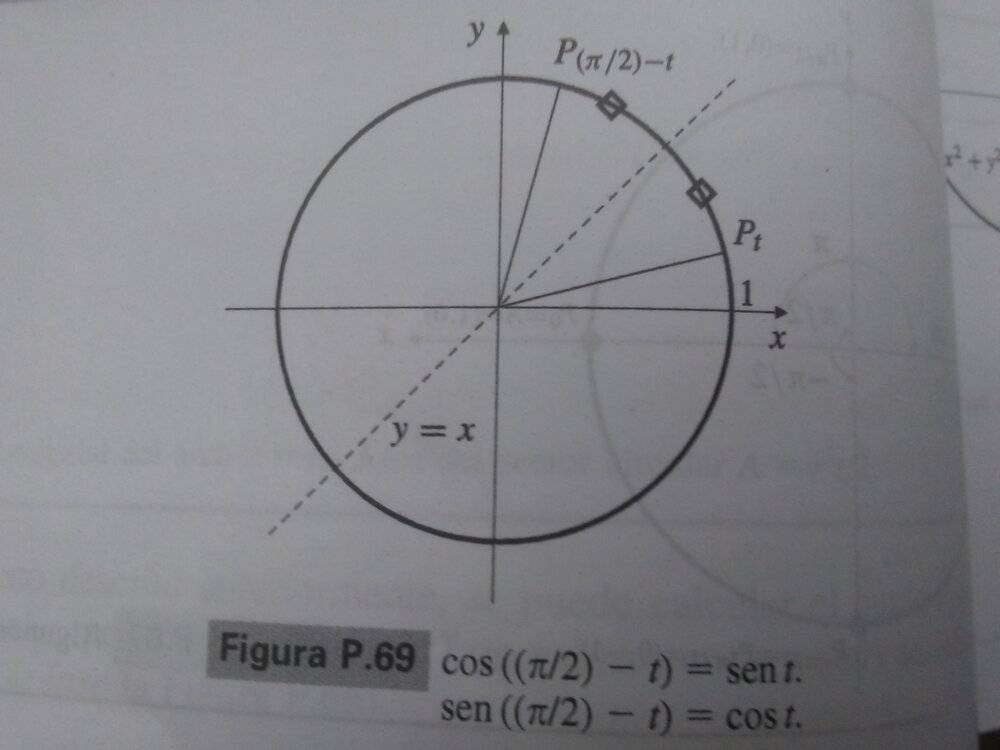
Identities of complementary angles
Two angles are complementary if they add up $\pi/2$ (or 90º). The points $P_{(\pi/2)-t}$ and $P_t$ are reflections (one of the other) about the line $y=x$ (Figura P.69), so the $x$ coordinate of one of them is the $y$ coordinate of the other, and vice versa. So
$\cos \left({\dfrac{\pi}´´ 2 -t\right)=\sin t$ and $\sin \left({\dfrac{\pi}2-t}\right)=\cos t$

Relevant Equations

Maybe Thales Theorem?

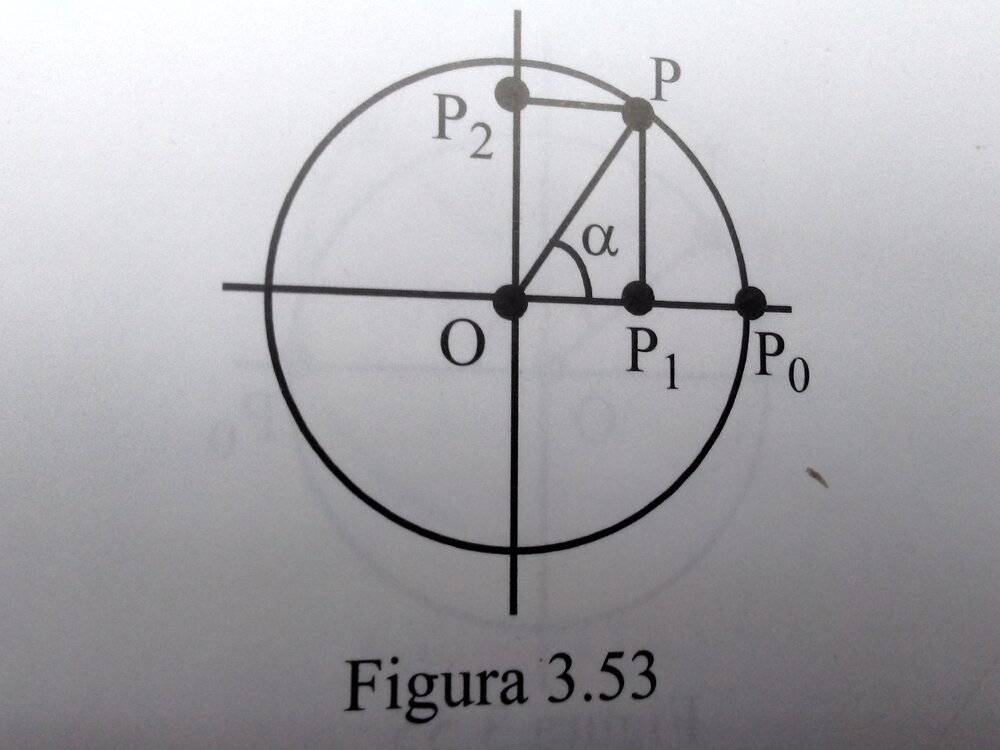
I thought I understood it until I found the statement mentioned. It's obvious having a look at Figura 3.53:

$\cos \alpha=\dfrac{OP_1}{OP}\Rightarrow{OP_1=\cos \alpha}$,

$\sin \alpha=\dfrac{OP_2}{OP}\Rightarrow{OP_2=OP\cos \left({\dfrac{\pi}{2}-\alpha}\right)=OP\sin \alpha}$

 

[PeroK]

Is there a question here?

 

[mcastillo356]

Processing...

 

[mcastillo356]

Well, it's all solved. It was the first time I faced the concept: a reflection can be thought of as a folding or "flipping" an object over the line of reflection. When I reflect a point across the line $y=x$, the $x$ coordinate and $y$ coordinate change places.
If I reflect over the line $y=-x$ the $x$ coordinate and $y$ coordinate change places and are negated (the signs are changed).
The reflection of the point $(x,y)$ across the line $y=x$ is the point $(y,x)$.
The reflection of the point $(x,y)$ across the line $y=-x$ is the point $(-y,-x)$