- #1
andyc10
- 5
- 0
I understand what is meant by the orthogonalilty of eigenfunctions...
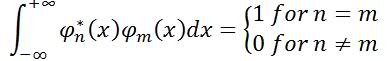
...but what is measnt by the completeness of eigenfunctions?
...but what is measnt by the completeness of eigenfunctions?
Avodyne said:[tex]\sum_n \varphi_n(x)\varphi^*_n(y)=\delta(x-y)[/tex]
ice109 said:or 1 for the space he's talking about
Hurkyl said:I can't figure out how that could make sense.
(Did you overlook that there's both an x and a y on the l.h.s.?)
Hurkyl said:It did give me pause, though, because I'm so unused to seeing distributions written "plainly" mixed with calculations done in Dirac notation.
i.e. I would have expected a calculation in Dirac notation to result in something that looked like [itex]|x\rangle\langle y|[/itex], which offers an unmatched ket and bra against which one can inner product away the distributional variables.
The completeness of eigenfunctions is a mathematical concept that states that a set of eigenfunctions for a given operator is able to represent any arbitrary function within the same domain.
The completeness of eigenfunctions is proven using mathematical techniques such as the Gram-Schmidt process and the Dirac delta function.
The completeness of eigenfunctions is important because it allows us to easily solve differential equations and other mathematical problems by using a set of eigenfunctions as a basis.
Yes, the completeness of eigenfunctions can be generalized to any operator as long as the operator is self-adjoint and the eigenfunctions form a complete set.
Yes, the completeness of eigenfunctions has various applications in physics, engineering, and other fields. For example, it is used in quantum mechanics to solve the Schrödinger equation and in signal processing to analyze and manipulate signals.