hsazerty2
- 2
- 1
Summary:: Inner Product Spaces, Orthogonality.
Hi there,
This my first thread on this forum :)
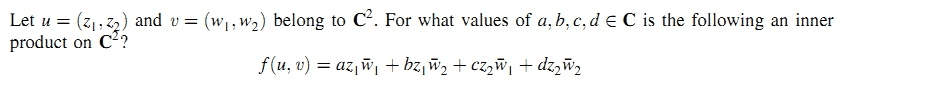
I encountered the above problem in Schaum’s Outlines of Linear Algebra 6th Ed (2017, McGraw-Hill) Chapter 7 - Inner Product Spaces, Orthogonality.
Using some particular values for u and v, I proved that a and d must be real positive, and b is the conjugate of c. The solution indicates that a.d-b.c must also be positive, but i can't figure that out.
thanks for your help.
[Moderator's note: Moved from a technical forum and thus no template.]
Hi there,
This my first thread on this forum :)
I encountered the above problem in Schaum’s Outlines of Linear Algebra 6th Ed (2017, McGraw-Hill) Chapter 7 - Inner Product Spaces, Orthogonality.
Using some particular values for u and v, I proved that a and d must be real positive, and b is the conjugate of c. The solution indicates that a.d-b.c must also be positive, but i can't figure that out.
thanks for your help.
[Moderator's note: Moved from a technical forum and thus no template.]
Last edited by a moderator:
