Complex-Linear Matrices & C-Linear Transformations .... Tapp, Propn 2.4 ....

[Math Amateur]

TL;DR

I am reading Kristopher Tapp's book: Matrix Groups for Undergraduates.

I am currently focused on and studying Section 1 in Chapter2, namely:

"1. Complex Matrices as Real Matrices".

I need help in fully understanding how to prove an assertion related to Tapp's Proposition 2.4.

I am reading Kristopher Tapp's book: Matrix Groups for Undergraduates.

I am currently focused on and studying Section 1 in Chapter2, namely:

"1. Complex Matrices as Real Matrices".

I need help in fully understanding how to prove an assertion related to Tapp's Proposition 2.4.

Proposition 2.4 and some comments following it read as follows:

In the remarks following Proposition 2.4 we read the following:

" ... ... It ($F$) is $\mathbb{C}$-linear if and only if $F(i \cdot X) = i \cdot F(X)$ for all $X \in \mathbb{C}^n$ ... "My question is as follows ... can someone please demonstrate a proof of the fact that $F$ is $\mathbb(C)$-linear if and only if $F(i \cdot X) = i \cdot F(X)$ for all $X \in \mathbb{C}^n$ ...
Help will be much appreciated ...

Peter===================================================================================
*** EDIT ***

After a little reflection it appears that " ... $F$ is $\mathbb{C}$-linear $\Longrightarrow F(i \cdot X) = i \cdot F(X)$ ... " is immediate as ...

... taking $c = i$ we have ...

$F(c \cdot X ) = c \cdot F(X) \Longrightarrow F(i \cdot X) = i \cdot F(X)$ for $c \in \mathbb{C}$Is that correct?

Peter

=======================================================================================
=======================================================================================

Note that Tapp defines$\rho_n$ and $f_n$ in the following text ... ...

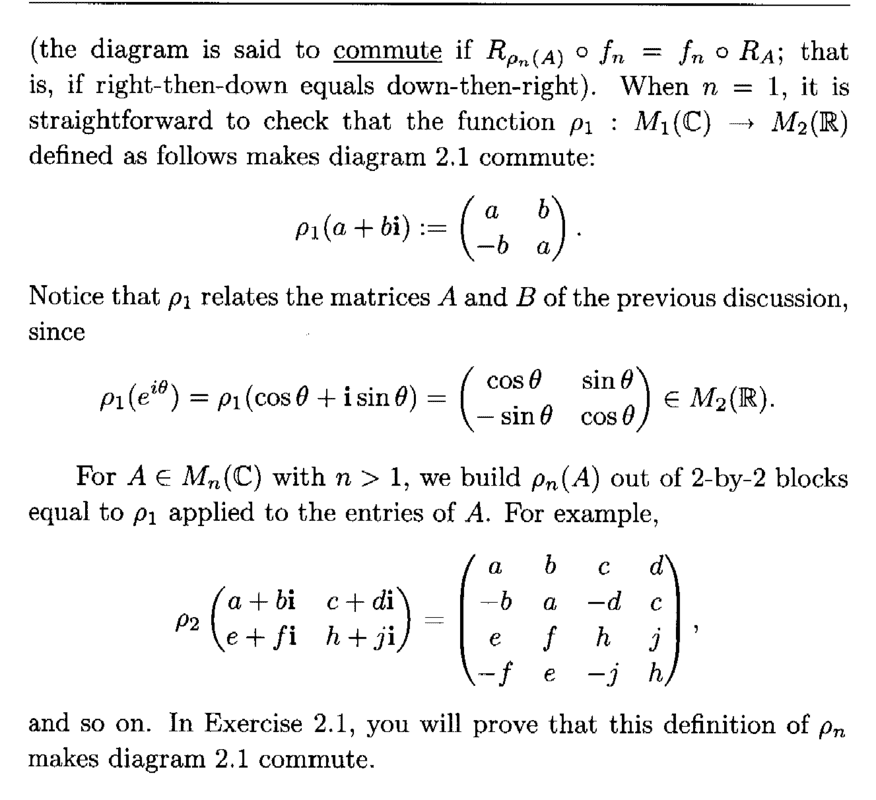
Also note that $R_B$ (actually $R_A$) is defined in the following text ...

Hope the provision of the above text helps with definitions, notation and context ...

Peter

 

[member 587159]

The proof uses that a map $T:V\to W$ between $\mathbb{C}$-vector spaces is $\mathbb{C}$-linear if and only if if $\mathbb{R}$-linear and $T(iv)=iT(v)$ for all $v\in V$.

From left to right is obvious by the definition, from right to left requires a little easy two-line proof.

Note that in the proof one says that $T$ is $\mathbb{C}$ linear if and only if $T(iv) = iT(v)$ for all $v\in V$ since it was already established that $T$ was $\mathbb{R}$-linear.

 

[Math Amateur]

The proof uses that a map $T:V\to W$ between $\mathbb{C}$-vector spaces is $\mathbb{C}$-linear if and only if if $\mathbb{R}$-linear and $T(iv)=iT(v)$ for all $v\in V$.

From left to right is obvious by the definition, from right to left requires a little easy two-line proof.

Note that in the proof one says that $T$ is $\mathbb{C}$ linear if and only if $T(iv) = iT(v)$ for all $v\in V$ since it was already established that $T$ was $\mathbb{R}$-linear.

Thanks for the post and the hint ...

We are considering $F \ : \ \mathbb{C}^n \to \mathbb{C}^n$ where $F = f_n^{ -1 } \circ R_B \circ f_n$ ...

We know that $F$ is $\mathbb{R}$-linear ... that is ...

$F(X + Y) = F(X) + F(Y)$ for all $X, Y \in \mathbb{C}^n$ ... ... ... ... ... (1)

... and ...

$F(rX) = r F(X)$ for all $X \in \mathbb{C}^n$ and $r \in \mathbb{R}$ ... ... ... ... ... (2)We have to prove that $F$ is $\mathbb{C}$-linear ... ...

... that is ...

$F(X + Y) = F(X) + F(Y)$ for all $X, Y \in \mathbb{C}^n$ ...

... which holds from the $\mathbb{R}$-linear case ...

and ...

$F(cX) = cF(X)$ for all $X \in \mathbb{C}^n$ and $c \in \mathbb{C}$ ... ... ... ... ... (3)So ... essentially we have to prove (3) ...

So then ... let $c = a + bi$ ... and proceed as follows ...

$F(cX) = F( (a+bi)X)$

$= F(aX + biX)$

$= F(aX) + F(biX)$ since $F$ is $\mathbb{R}$-linear

$= F(aX) + iF(bX)$ since $F(iY) = iF(Y)$

$= aF(X) + biF(X)$ since $F$ is $\mathbb{R}$-linear

$= (a +bi)F(X)$

$= cF(X)$Hope the above is correct ... ...

Peter

 

[member 587159]

Thanks for the post and the hint ...

We are considering $F \ : \ \mathbb{C}^n \to \mathbb{C}^n$ where $F = f_n^{ -1 } \circ R_B \circ f_n$ ...

We know that $F$ is $\mathbb{R}$-linear ... that is ...

$F(X + Y) = F(X) + F(Y)$ for all $X, Y \in \mathbb{C}^n$ ... ... ... ... ... (1)

... and ...

$F(rX) = r F(X)$ for all $X \in \mathbb{C}^n$ and $r \in \mathbb{R}$ ... ... ... ... ... (2)We have to prove that $F$ is $\mathbb{C}$-linear ... ...

... that is ...

$F(X + Y) = F(X) + F(Y)$ for all $X, Y \in \mathbb{C}^n$ ...

... which holds from the $\mathbb{R}$-linear case ...

and ...

$F(cX) = cF(X)$ for all $X \in \mathbb{C}^n$ and $c \in \mathbb{C}$ ... ... ... ... ... (3)So ... essentially we have to prove (3) ...

So then ... let $c = a + bi$ ... and proceed as follows ...

$F(cX) = F( (a+bi)X)$

$= F(aX + biX)$

$= F(aX) + F(biX)$ since $F$ is $\mathbb{R}$-linear

$= F(aX) + iF(bX)$ since $F(iY) = iF(Y)$

$= aF(X) + biF(X)$ since $F$ is $\mathbb{R}$-linear

$= (a +bi)F(X)$

$= cF(X)$Hope the above is correct ... ...

Peter

Yes, completely correct. Well done!