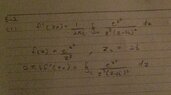aruwin
- 204
- 0
Hello.
I am not confident about this question. I think I have to use cauchy integral formula. But before that, I should decompose the fraction, right? Or is there a simpler way to do it? A friend told me that each contour only had one pole interior to it so he just used the Cauchy integral formula for the appropriate derivatives--as opposed to using a residue calculus. Is this a correct method?
I am not confident about this question. I think I have to use cauchy integral formula. But before that, I should decompose the fraction, right? Or is there a simpler way to do it? A friend told me that each contour only had one pole interior to it so he just used the Cauchy integral formula for the appropriate derivatives--as opposed to using a residue calculus. Is this a correct method?