- #1
DoobleD
- 259
- 20
I have some conceptual issues with functions in vectors spaces. I don't really get what are really the components of the vector / function.
When we look at the inner product, it's very similar to dot product, as if each value of a function was a component :
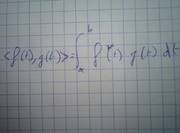
So I tend to think to f(t) as the vector whose components are : (f(1), f(2), ..., f(n)).
But a function can also be approximated as a series of some constants times a base function from an orthonormal set spaning the space. Quite like a vector in 3D for instance, with constants times unit vectors, but with possibly an infinity of dimensions, and base functions instead of unit vectors. Like so (Cn is a constant, Un is a base function) :
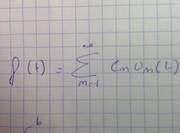
Then I'm like : uh, so, what are the vector-like components of a function ? Are they the values of the function, f(t), or the constants Cn ? Which one is it ? It can't be both (I think) because those are simply not the same thing. f(3) != C3.
When we look at the inner product, it's very similar to dot product, as if each value of a function was a component :
So I tend to think to f(t) as the vector whose components are : (f(1), f(2), ..., f(n)).
But a function can also be approximated as a series of some constants times a base function from an orthonormal set spaning the space. Quite like a vector in 3D for instance, with constants times unit vectors, but with possibly an infinity of dimensions, and base functions instead of unit vectors. Like so (Cn is a constant, Un is a base function) :
Then I'm like : uh, so, what are the vector-like components of a function ? Are they the values of the function, f(t), or the constants Cn ? Which one is it ? It can't be both (I think) because those are simply not the same thing. f(3) != C3.