What is Vector spaces: Definition and 283 Discussions

A vector space (also called a linear space) is a set of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms (listed below in § Definition). To specify that the scalars are real or complex numbers, the terms real vector space and complex vector space are often used.
Certain sets of Euclidean vectors are common examples of a vector space. They represent physical quantities such as forces, where any two forces (of the same type) can be added to yield a third, and the multiplication of a force vector by a real multiplier is another force vector. In the same way (but in a more geometric sense), vectors representing displacements in the plane or three-dimensional space also form vector spaces. Vectors in vector spaces do not necessarily have to be arrow-like objects as they appear in the mentioned examples: vectors are regarded as abstract mathematical objects with particular properties, which in some cases can be visualized as arrows.
Vector spaces are the subject of linear algebra and are well characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. Infinite-dimensional vector spaces arise naturally in mathematical analysis as function spaces, whose vectors are functions. These vector spaces are generally endowed with some additional structure such as a topology, which allows the consideration of issues of proximity and continuity. Among these topologies, those that are defined by a norm or inner product are more commonly used (being equipped with a notion of distance between two vectors). This is particularly the case of Banach spaces and Hilbert spaces, which are fundamental in mathematical analysis.
Historically, the first ideas leading to vector spaces can be traced back as far as the 17th century's analytic geometry, matrices, systems of linear equations and Euclidean vectors. The modern, more abstract treatment, first formulated by Giuseppe Peano in 1888, encompasses more general objects than Euclidean space, but much of the theory can be seen as an extension of classical geometric ideas like lines, planes and their higher-dimensional analogs.
Today, vector spaces are applied throughout mathematics, science and engineering. They are the appropriate linear-algebraic notion to deal with systems of linear equations. They offer a framework for Fourier expansion, which is employed in image compression routines, and they provide an environment that can be used for solution techniques for partial differential equations. Furthermore, vector spaces furnish an abstract, coordinate-free way of dealing with geometrical and physical objects such as tensors. This in turn allows the examination of local properties of manifolds by linearization techniques. Vector spaces may be generalized in several ways, leading to more advanced notions in geometry and abstract algebra.
This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces.

View More On Wikipedia.org
Recent contents Top users
  1. I

    What is meant by compex dimension? (Abstract algebra)

    picture since the text is a little hard to read i have no problem showing this is a vector space, but what is meant by complex dimention? Is it just the number on independant complex numbers, so n?
  2. K

    I ##\mathbb{C}\oplus\mathbb{C}\cong\mathbb{C}\otimes\mathbb{C}##

    Hello! Reading book o Clifford algebra authors claim that ##\mathbb{C}\oplus\mathbb{C}\cong\mathbb{C}\otimes_{\mathbb{R}}\mathbb{C}## as algebras. Unfortunately proof is absent and provided hint is pretty misleading As vector spaces they are obviously isomorphic since ##\dim_{\mathbb{R}}...
  3. robphippen

    I Understanding Spin States in 2D Vector Spaces

    There is a passage in this book where I don't follow the logic; In this short quotation from 'Quantum Mechanics: The Theoretical Minimum' by Leonard Susskind and Art Friedman \mathcal{A} represents the apparatus that is performing the measurement the apparatus can be oriented (in principle) in...
  4. H

    Vector space of functions defined by a condition

    ##f : [0,2] \to R##. ##f## is continuous and is defined as follows: $$ f = ax^2 + bx ~~~~\text{ if x belongs to [0,1]}$$ $$ f(x)= Ax^3 + Bx^2 + Cx +D ~~~~\text{if x belongs to [1,2]}$$ ##V = \text{space of all such f}## What would the basis for V? Well, for ##x \in [0,1]## the basis for ##V##...
  5. pellis

    A How to visualise complex vector spaces of dimension 2 and above

    According to e.g. Keith Conrad (https://kconrad.math.uconn.edu/blurbs/ choose Complexification) If W is a vector in the vector space R2, then the complexification of R2, labelled R2(c), is a vector space W⊕W, elements of which are pairs (W,W) that satisfy the multiplication rule for complex...
  6. nomadreid

    I Shouldn't this definition of a metric include a square root?

    In https://mathworld.wolfram.com/InnerProduct.html, it states "Every inner product space is a metric space. The metric is given by g(v,w)= <v-w,v-w>." In https://en.wikipedia.org/wiki/Inner_product_space , on the other hand, "As for every normed vector space, an inner product space is a metric...
  7. Santiago24

    I Two ways to define operations in a vector space

    Hi PF, I've one question about vector spaces. There is only one way to define the operations of a vector space? For example if V is a vector space there is other way to define their operations like scalar multiplication or the sums of their elements and that the result is also a vector space?
  8. L

    A What Topological Vector Spaces have an uncountable Schauder basis?

    Let ##P## be an uncountable locally finite poset, let ##F## be a field, and let ##Int(P)=\{[a,b]:a,b\in P, a\leq b\}##. Then the incidence algebra $I(P)$ is the set of all functions ##f:P\rightarrow F##, and it's a topological vector space over ##F## (a topological algebra in fact) with an...
  9. S

    Vector space of linear maps

    Solution 1. Based on my analysis, elements of ##V## is a map from the set of numbers ##\{1, 2, ..., n\}## to some say, real number (assuming ##F = \mathbb{R}##), so that an example element of ##F## is ##x(1)##. An example element of the vector space ##F^n## is ##(x_1, x_2, ..., x_n)##. From...
  10. K

    What can we say about the eigenvalues if ##L^2=I##?

    This was a problem that came up in my linear algebra course so I assume the operation L is linear. Or maybe that could be derived from given information. I don't know how though. I don't quite understand how L could be represented by anything except a scalar multiplication if L...
  11. LCSphysicist

    Proofs in analytic geometry and vector spaces.

    I was just thinking, if is said to me demonstrate any geometry statement, can i open the vector in its vector's coordinates? I will say more about: For example, if is said to me: Proof the square's diagonals are orthogonal, how plausible is a proof like?: d1 = Diagonal one = (a,b,c) d2 =...
  12. vanhees71

    A Affine Spaces and Vector Spaces

    [Moderator's Note: Spun off from previous thread due to increase in discussion level to "A" and going well beyond the original thread's topic.] A vector space has no origin to begin with ;-)). An affine space is a set of points and a vector space ##(M,V)##. Then you have a set of axioms which...
  13. S

    Proof of isomorphism of vector spaces

    The theorem is as follows: All finite dimensional vector spaces of the same dimension are isomorphic Attempt: If T is a linear map defined as : T : V →W : dim(V) = dim(W) = x < ∞ & V,W are vector spaces It would be sufficient to prove T is a bijective linear map: let W := {wi}ni like wise let...
  14. I

    [Linear Alg] Determining which sets are subspaces of R[x]

    Homework Statement [/B] Which of the following sets are subspaces of ##R[x]?## ##W_1 = {f \in \mathbf R[x] : f(0) = 0}## ##W_2 = {f \in \mathbf R[x] : 2f(0) = f(1)}## ##W_3 = {f \in \mathbf R[x] : f(t) = f(1-t) \forall t \in \mathbf R}## ##W_4 = {f \in \mathbf R[x] : f = \sum_{i=0}^n...
  15. I

    Determining if a subset W is a subspace of vector space V

    Homework Statement Let V = RR be the vector space of the pointwise functions from R to R. Determine whether or not the following subsets W contained in V are subspaces of V. Homework Equations W = {f ∈ V : f(1) = 1} W = {f ∈ V: f(1) = 0} W = {f ∈ V : ∃f ''(0)} W = {f ∈ V: ∃f ''(x) ∀x ∈ R} The...
  16. Mr Davis 97

    I Difference between R^n and other vector spaces

    I feel like the vector space ##\mathbb{R}^n## differs from other vector spaces, like ##\mathbb{P}##. For example, if we wrote down an element of ##\mathbb{P}##, like ##1+2t^2##, this is an object in its own right, with no reference to any coordinate system or basis. However, when I write down an...
  17. M

    MHB Question on vector spaces

    Could we have two vector spaces each with its own set of basis vectors. but these basis vectors are related according to the following way. A particular set of vectors in the first vector space may exist "all over the place" but when you represent the same information in the second vector space...
  18. K

    I Vector spaces and subspaces

    Does it make sense to say that a set together with a field generates a vector space? I came across this question after starting the thread https://www.physicsforums.com/threads/determine-vector-subspace.941424/ To be more specific, suppose we have a set consisting of two elements ##A = \{x^2, x...
  19. F

    I Operators and vectors in infinite dimensional vector spaces

    Hello Everyone. I am searching for some clarity on this points. Thanks for your help: Based on Schrodinger wave mechanics formulation of quantum mechanics, the states of a system are represented by wavefunctions (normalizable or not) and operators (the observables) by instructions i.e...
    • fog37
    • Thread
    • Infinite Operators Vector Vector spaces Vectors
    • Replies: 3
    • Forum: Quantum Physics
  20. F

    I Understanding Hilbert Vector Spaces

    Hello, I think I understand what a vector space is. It is inhabited by objects called vectors that satisfy a certain number of properties. The vectors can be functions whose integral is not infinite, converging sequences, etc. The vector space can be finite dimensional or infinite dimensional...
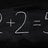
  21. Alex Langevub

    Is the zero Matrix a vector space?

    Homework Statement So I have these two Matrices: M = \begin{pmatrix} a & -a-b \\ 0 & a \\ \end{pmatrix} and N = \begin{pmatrix} c & 0 \\ d & -c \\ \end{pmatrix} Where a,b,c,d ∈ ℝ Find a base for M, N, M +N and M ∩ N. Homework Equations I know the 8 axioms about the vector spaces. The...
  22. peroAlex

    Vector Spaces Question

    Hello, everybody! I would really appreciate if someone could help me understand how to solve the following two tasks. I am not sure whether my translation is correct, so if, by any chance, you know a more appropriate terminology, please let me know. I am not fluent in writing matrices here on...
  23. FallenApple

    I Advantages of Vector Spaces over Modules

    I know that vector spaces have more structure as they are defined over fields and that modules are defined over rings. But it's hard to think of a situation where a using a ring clearly backfires. Is it just because a ring doesn't have an inverse for the second operation? For a module over Z...
  24. fresh_42

    Insights What Is a Tensor? - Comments

    fresh_42 submitted a new PF Insights post What Is a Tensor? Continue reading the Original PF Insights Post.
  25. B

    B Vector Space over Field of Real Numbers

    I am confused why is space over field ##R## not over field ##C## ? The entries in each vector is an element of ##\Bbb C## not ##\Bbb R##.
  26. S

    Shankar Exercise 1.1.3 (Vector Spaces)

    <Mentor's note: moved from a technical forum, therefore no template.> I'm long out of college and trying to teach myself QM out of Shankar's. I'm trying to understand the reasoning here because I think that I am missing something... 1.1.3 1) Do functions that vanish at the endpoints x=0 and...
  27. Austin Chang

    I Understanding Vector Spaces with functions

    Is the set of all differentiable functions ƒ:ℝ→ℝ such that ƒ'(0)=0 is a vector space over ℝ? I was given the answer yes by someone who is better at math than me and he tried to explain it to me, but I don't understand. I am having difficulty trying to conceptualize this idea of vector spaces...
  28. Austin Chang

    I Vector Spaces Question

    In a vector space can you limit the scalar. For example, if I have Vector space in ℤ2 can i only multiple integer scalars?
  29. F

    I State Representation in QM and Vector Spaces

    Hello Forum, The state of a quantum system is indicated by##\Psi## in Dirac notation. Every observable (position, momentum, energy, angular momentum, spin, etc.) corresponds to a linear operator that acts on ##\Psi##.Every operator has its own set of eigenstates which form an orthonormal basis...
    • fog37
    • Thread
    • Qm Representation State Vector Vector spaces
    • Replies: 4
    • Forum: Quantum Physics
  30. A

    I Prove the sequence is exact: 0 → ker(f) → V → im(f) → 0

    Problem: Let f ∶ V → V be a linear operator on a finite-dimensional vector space V . Prove that the sequence 0 → ker(f) → V → im(f) → 0 is exact at each term. Attempt: If I call: a: 0 → ker(f), b: ker(f) → V, c: V → im(f), d: im(f) → 0. Then the sequence is exact at: ker(f) if...
  31. M

    MHB Are these vector spaces?

    Hey! :o I want to check if the following are true. $V_1=\{a\in \mathbb{R}\mid a>0\}$ with the common multiplication as the vector addition and the scalar multiplication $\lambda \odot v=v^{\lambda}$ is a $\mathbb{R}$-vector space. $V_2=\{(x,y)\in \mathbb{Q}^2 \mid x^2=-y^2\}$ with the...
  32. K

    MHB Some basic question about vector spaces

    I need some help understanding one task. I know that for some structure to be a vector space all axioms should apply. So if any of those axioms fails then the given structure is not a vector space. Anyway, I have a task where I need to check if \mathbb{C}^n_\mathbb{R} is a vector space. But, I...
  33. ShayanJ

    A For finite dimension vector spaces, all norms are equivalent

    I searched for a proof of the statement in the title and found this document. But it just proves that for two norms ## \rho(x) ## and ## ||x|| ##, we have ## m\rho(x)\leq ||x|| \leq M \rho(x) ## for some m and M. But how does it imply that the two norms are equivalent? Thanks
  34. DoobleD

    I Components of functions in vector spaces

    I have some conceptual issues with functions in vectors spaces. I don't really get what are really the components of the vector / function. When we look at the inner product, it's very similar to dot product, as if each value of a function was a component : So I tend to think to f(t) as the...
  35. B

    I Normed Vector Spaces and Topological Vector Spaces

    Let ##(V, ||\cdot||)## be some finite-dimensional vector space over field ##\mathbb{F}## with ##\dim V = n##. Endowing this vector space with the metric topology, where the metric is induced by the norm, will ##V## become a topological vector space? It seems that this might be true, given that...
  36. R

    I Vector Transformation Law and Vector Spaces: Is it Abuse?

    Typically an element of a vector space is called a vector, but Carroll's GR book repeatedly refers to elements of tangent spaces as "transforming as a vector" when they change coordinates as Vμ = ∂xμ/∂xν Vν. However, dual vectors are members of vector spaces (cotangent space) but obey ωμ =...
  37. E

    I Axiom 10 of Vector Spaces

    So I understand how to prove most of the axioms of a vector space except for axiom 10, I just do not understand how any set could fail the Scalar Identity axiom; Could anybody clarify how exactly a set could fail this as from what I know that anything times one results in itself 1u = u...
  38. Prof. 27

    Showing that Something is a Subspace of R^3

    Homework Statement The question asks to show whether the following are sub-spaces of R^3. Here is the first problem. I want to make sure I'm on the right track. Problem: Show that W = {(x,y,z) : x,y,z ∈ ℝ; x = y + z} is a subspace of R^3. Homework Equations None The Attempt at a Solution...
  39. K

    Direct Sum: Vector Spaces

    During lecture, the professor gave us a theorem he wants us to prove on our own before he goes over the theorem in lecture. Theorem: Let ##V_1, V_2, ... V_n## be subspaces of a vector space ##V##. Then the following statements are equivalent. ##W=\sum V_i## is a direct sum. Decomposition of...
  40. G

    Modular arithmetic on vector spaces

    Homework Statement Let U is the set of all polynomials u on field \mathbb F such that u(3)=u(-2)=0. Check if U is the subspace of the set of all polynomials P(x) on \mathbb F and if it is, determine the set W such that P(x)=U\oplus W. Homework Equations -Polynomial vector spaces -Subspaces...
  41. G

    Linear algebra: Prove the statement

    Homework Statement Prove that \dim L(\mathbb F)+\dim Ker L=\dim(\mathbb F+Ker L) for every subspace \mathbb{F} and every linear transformation L of a vector space V of a finite dimension. Homework Equations -Fundamental subspaces -Vector spaces The Attempt at a Solution Theorem: [/B]If...
  42. Math Amateur

    MHB Vector Spaces .... Linear Dependence and Indepence .... Basic Proof Required

    In Andrew McInerney's book: First Steps in Differential Geometry, Theorem 2.4.3 reads as follows: https://www.physicsforums.com/attachments/5252 McInerney leaves the proofs for the Theorem to the reader ... I am having trouble formulating a proof for Part (3) of the theorem ... Can someone...
  43. G

    Finite dimensional normed vector spaces complete ?

    Homework Statement Show that finite dimensional normed vector spaces are complete. Homework Equations ##E## is a finite dimensional vector space and ##N## a norm on ##E## The Attempt at a Solution If ##\{x_n\}_n## is a Cauchy sequence in ##(E,N)##, then it is bounded and each term of the...
  44. Math Amateur

    MHB Two Versions of the Correspondence Theorem for Vector Spaces

    Cooperstein (in Advanced Linear Algebra) and Roman (also in a book called Advanced Linear Algebra) give versions of the Correspondence Theorem for Vector Spaces ... but these 'versions' do not look like the same theorem ... can someone please explain how/why these two versions are actually the...
  45. G

    Linear algebra: Finding a basis for a space of polynomials

    Homework Statement Let and are two basis of subspaces and http://www.sosmath.com/CBB/latexrender/pictures/69691c7bdcc3ce6d5d8a1361f22d04ac.png. [Broken] Find one basis of http://www.sosmath.com/CBB/latexrender/pictures/38d4e8e4669e784ae19bf38762e06045.png and...
  46. Math Amateur

    MHB Understand Theorem 2.15 - Bruce Cooperstein's Advanced Linear Algebra

    I am reading Bruce Cooperstein's book: Advanced Linear Algebra ... ... I am focused on Section 2.3 The Correspondence and Isomorphism Theorems ... ... I need further help with understanding Theorem 2.15 ... Theorem 2.15 and its proof read as follows...
  47. Math Amateur

    MHB Correspondence Theorem for Vector Spaces - Cooperstein Theorem 2.15

    I am reading Bruce Cooperstein's book: Advanced Linear Algebra ... ... I am focused on Section 2.3 The Correspondence and Isomorphism Theorems ... ... I need help with understanding Theorem 2.15 ... Theorem 2.15 and its proof read as follows: It appears to me (and somewhat surprises...
  48. Math Amateur

    MHB Vector Spaces and Linear Transformations - Cooperstein Theorem 2.7

    I am reading Bruce Cooperstein's book: Advanced Linear Algebra ... ... I am focused on Section 2.1 Introduction to Linear Transformations ... ... I need help with understanding Theorem 2.7 ... Theorem 2.7, its proof and some remarks read as follows: I am having considerable trouble...
  49. Math Amateur

    MHB Vector Spaces - The Exchange Theorem - Cooperstein Theorem 1.16

    I am reading Bruce Cooperstein's book: Advanced Linear Algebra ... ... I am focused on Section 1.6 Bases and Finite-Dimensional Vector Spaces ... I need help with the proof of Theorem 1.16 ... Theorem 1.16 and its proof reads as follows: Question 1 In the second paragraph of above...
  50. Math Amateur

    MHB Basic Exercise in Vector Spaces - Cooperstein Exercise 2, page 14

    I am reading Bruce Cooperstein's book: Advanced Linear Algebra ... ... I am focused on Section 1.3 Vector Spaces over an Arbitrary Field ... I need help with Exercise 2 of Section 1.3 ... Exercise 2 reads as follows: Hope someone can help with this exercise ... Peter *** EDIT ***...
Back
Top