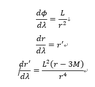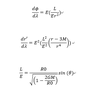Computational physics - Light trajectory near black hole

[PhysicsMajorLeo]

Dear all,

I am currently doing a project about the light trajectory near Schwarzschild black hole. I wrote down a couple of differential equation and I have created a C++ program hoping to solve the orbit of light. However, the program results turn out to be quite weird.

The differential equation needed to be solved:

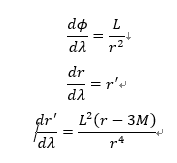
Where r is the radial position and phi is the azimuthal angle, L is the angular momentum of the photon.

The first thing I noticed is that sometimes, depending on initial conditions, the results sometimes turns out to be negative in r, even if r is positive, the change in r is so small that it remains in order of 10^-5, and the change in phi is also small. Nevertheless the program always produce diverging results in r. I think I may be misunderstanding the physical picture of the equation.

I would like to ask does the equation describing the motion of a photon launching at a arbitrary position? Furthermore, what is the typical value of L in the Geometrized unit system? Furthermore, I know that the impact parameter b is related to L and energy of photon e by b=L/e, is there any ways to simplify the above differential equation so that I could get a differential equation only depends on b? Thank you!

 

[Ibix]

Furthermore, what is the typical value of L in the Geometrized unit system?

See https://www.physicsforums.com/threads/null-geodesics-in-schwarzschild-spacetime.895174/

Note that my initial post is incorrect - do read all the way down. As you say, you can write L in terms of E, which is the photon energy at infinity (which has no effect on the trajectory - it just scales $\lambda$), and the angle at which it is launched.

 

[mfb]

I would like to ask does the equation describing the motion of a photon launching at a arbitrary position?

I'm not sure if the equations are fully correct but they should reproduce all the interesting features of the motion of light, so it looks like they are right.

urthermore, what is the typical value of L in the Geometrized unit system?

I don't think "typical value" is a useful concept for the actual angular momentum (a photon with a different energy will follow the same trajectory while having a different angular momentum), and in the way it appears in the equations it looks like an overall scaling factor only. To get different trajectories, start with different r and/or r'.

 

[PhysicsMajorLeo]

See https://www.physicsforums.com/threads/null-geodesics-in-schwarzschild-spacetime.895174/

Note that my initial post is incorrect - do read all the way down. As you say, you can write L in terms of E, which is the photon energy at infinity (which has no effect on the trajectory - it just scales $\lambda$), and the angle at which it is launched.

Thanks for the reply Ibix, I have read through the passage, I think I understand how the initial conditions on L could be altered. In the post, you stated that E is just a scaling factor which do not affect the orbit, and that the ratio of L/E is the one that is important. Also, George also state that it is easier to divide the equation into two coupled differential equation, combining results, I get the following:

Where theta is the initial value of launching angle, R0 is the initial radial position from the center

Where I could substitute L/E back into the ode, and since E is just a scaling factor, Could I just set E=1? Thanks!

I'm not sure if the equations are fully correct but they should reproduce all the interesting features of the motion of light, so it looks like they are right.I don't think "typical value" is a useful concept for the actual angular momentum (a photon with a different energy will follow the same trajectory while having a different angular momentum), and in the way it appears in the equations it looks like an overall scaling factor only. To get different trajectories, start with different r and/or r'.

Thanks for the reply mfb. Indeed, as stated in the book of Hartle, the trajectory of photon could only depends on the ratio L/E but not L or E individually, so I was very confused when I saw the factor L in the differential equation in the op. But after getting the advise from Ibix, I think I could get rid of it, do you think this modification is reasonable? Thanks!

 

[mfb]

Now you have L/E and E in the equations. I think you have to rescale $\lambda$ to get rid of it.

 

[PhysicsMajorLeo]

Now you have L/E and E in the equations. I think you have to rescale $\lambda$ to get rid of it.

Thanks for the relpy mfb. I think I can get rid of L/E by definition(the 3rd row),but I am not able to get rid of E in this case.

 

[mfb]

Well, the third row gives you L/E as function of the initial conditions.
Changing E shouldn't change the photon trajectory, so you can probably set it to whatever you like.

 

[Ibix]

I regarded E as a scale factor, basically. Changing it can be countered by changing the affine parameter by the same factor, which tells you it doesn't matter. The point about L/E is that it is simply a measure of what fraction of the light's momentum is pointing in the tangential direction. In flat space it would simply be $\sin\theta$ times appropriate constants for the units (note that in my thread I used $\psi$ for this angle because $\theta$ is already in use as a coordinate). In curved spacetime, however, you also need an extra factor to relate local angle measures to the coordinates, which is where the square root prefactor comes in.